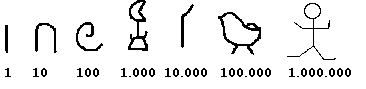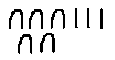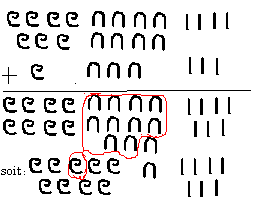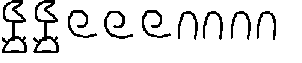Introduction - Les papyrus - Les
différents signes -
Origine probable des symboles -
Fractions
- Addition -
Multiplication par 10 - Multiplication -
division
Apparition
: environ 3.000 ans avant JC
numération
: additive et
de base 10 .
Ni
existence , ni nécessité d'un zéro
, puisque la numération est additive.
Les
Egyptiens reproduisaient les chiffres en les gravant ou en les sculptant
sur des
monuments de pierre ou sur des roches, au moyen du ciseau ou du marteau ;
ou encore sur des feuilles de papyrus ( le papyrus est une plante voisine
du roseau découpée en bandes , puis collées bout à
bout et enfin enroulées sur un bâton de bois ) , à l'aide d'un
roseau à pointe écrasée trempée dans une matière colorante.
Les
scribes égyptiens de l'époque des pharaons ( de 3.000 ans avant JC à 300 ans
avant JC ) utilisaient un hiéroglyphe pour désigner chacun des nombres : 1
; 10 ; 100 ; 1000 ; 10.000 ; 100.000 et 1.000.000 . On peut ainsi écrire les
nombres jusqu'à 999.999.999
Ils
utilisaient un système de numération à base 10 de type additif : pour écrire
le chiffre 7 par exemple , à la différence de notre système d'écriture , ils
répétaient le symbole de l'unité sept fois .
Il
existait deux systèmes d'écriture : le système hiéroglyphique utilisé
pour les monuments et les pierres tombales ( chaque symbole représente un
objet ) et le système hiératique ( simplification des hiéroglyphes ) utilisé
sur les papyrus dont le plus célèbre est le papyrus Rhind datant
du XVIIIe siècle avant JC : il fut écrit par le scribe Ahmès
et fut acheté au XIXe siècle en Egypte par un anglais du nom
de Rhind .
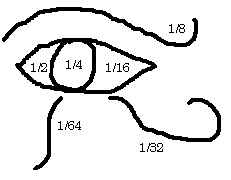
Pour
mesurer les capacités ( céréales , fruits , liquides
) , les Egyptiens utilisaient le héqat ( soit environ 4 ,785 litres
) et notaient les fractions en utilisant les parties de l'oeil fardé
du dieu faucon Horus , oeil moitié humain , moitié faucon
.Horus est le fils unique d'Isis et Osiris .
En
ce qui concerne les opérations , ils possédaient des tables
de racines carrées , de puissances succesives ; ils savaient extraire
les racines carrées et cubiques ; ils savaient résoudre une
équation du premier ou du deuxième degré à une
inconnue , mais aussi un système d'équations du premier degré
à deux inconnues .
Les
Egyptiens sont très probablement à l'origine de la géométrie:
lors de chaque crue du Nil , ils devaient retrouver les parcelles de chacun
( en forme de triangle , rectangle ) .Les "métreurs" (personnes
qui étaient chargées de reformer les parcelles) utilisaient
la cordelette à 13 noeuds pour tracer des angles droits et ont déterminé
des surfaces de terrains.
Les papyrus étant un matériau très fragile , peu ont été retrouvés ; parmi eux le " papyrus Rhind " et le " papyrus de Moscou " .
Le
papyrus Rhind a été rédigé vers 1650 avant
JC par un scribe nommé Ahmès ; ce dernier a recopié un
original vieux de deux siècles . Il rassemble 87 problèmes avec
leurs solutions et est rédigé en écriture hiératique
ordinaire. La plupart de ces problèmes sont des problèmes :
répartition de neuf pains entre dix personnes.( Les Egyptiens ne connaissaient
pas la monnaie et utilisaient un système d' échanges de biens
( essentiellement le pain et la bière ) . On y trouve aussi une méthode
pour calculer l'aire d'un triangle rectangle , aucune formule générale
n'est donnée. Ce papyrus ne contient pas de problèmes du second
degré.
Le papyrus Rhind aurait été découvert à Thèbes au milieu du XIXe siècle . Il fut acheté à Louksor par Rhind et revendu au British Museum à Londres par ses exécuteurs testamentaires. Sur le morceau ci-dessus , il s'agit d'un problème de calculs d'aires à l'intérieur d'un terrain triangulaire. Il est conservé en deux fragments : l'un de 2 mètres et l'autre de 2,95 mètres de long sur 32 cm de large.Il manque environ 20 cm entre les deux fragments , une partie de ce fragment manquant est conservée à New-York.
Le
papyrus de Moscou traite à peu près des mêmes sujets
; il contient aussi le calcul du volume du tronc de pyramide à base
carrée et de ce qui semble être l'aire de l'hémisphère.Ce
papyrus contient dont quatre portent sur la géométrie .
Le
papyrus de Kahun date de 1800 avant JC environ. Il contient une table
de quatre carrés présentés comme la somme des deux autres
carrés :
6 ² + 8² = 10 ² ; 12 ² + 16 ² = 20 ² ; ( 1 1/2 ) ² + 2 ² = ( 2 1/2 ) ² ; ( 3 / 4 ) ² + 1 ² = ( 1 1/4 ) ²
Les nombres sont obtenus à partir de 3 ; 4 et 5 par duplications successives et par divisions par deux successives
Les
connaissances des Egyptiens :
a
une origine naturelle 
peut
être un cordon servant à relier des bâtonnets pour en faire un paquet de 10
unités.
fleur
de lotus : probablement un emprunt phonétique signifiant " mille "
.
Il existait cependant trois fractions particulières : 
devient
:
12 
45 