La notation 
est due à Adrien Romain , au XVIe siècle
. Il a choisi car c’est la première lettre du mot grec « 
» ( se lit
« peripheria ») qui signifie circonférence .
3,141 592 653 589 793 238 462 643 383 279
...
est dûe à Archimède " Dans tout cercle , la proportion
de la circonférence au diamètre et la proportion de la superficie
au carré du rayon sont égales à une même constante
" .
Qui a calculé les décimales de et comment ?
C’est Archimède
, mathématicien grec , qui a trouvé une méthode pour calculer les décimales
de .
En calculant le rapport
entre le périmètre d’un cercle et son diamètre ( le périmètre étant mesuré
à l’aide d’une ficelle ).
Il s’aperçut qu’on trouvait toujours le même nombre à quelques
décimales près .
Archimède prit donc le cas du cercle de diamètre 1 ( dans
ce cas , le périmètre est égal à ) ;
il a « encadré » le cercle par deux polygones à 96 côtés , et il
a calculé le périmètre de ces deux polygones .
Ainsi , vers 250 avant JC , il montre que est
compris entre 
et
.
Grâce à sa méthode , on a pu déterminer les décimales de .
En 1949 , le premier
ordinateur , l'ENIAC, calcula 2000 décimales de
en 70 heures .
Grâce à de puissants ordinateurs , Yasumasa Kanada a pu calculer
plus de 6 442 450 938 décimales de en
1995, et ce après 116 heures de calcul et 131 heures de vérification
de l'ordinateur .
ü Méthode
d’Archimède pour calculer les décimales de :
Sa méthode consiste à encadrer un cercle de rayon 1 par deux
polygones réguliers inscrits et
circonscrits à ce cercle . Archimède a considéré successivement
des polygones à 6 ; 12 ;
24 ; 48
et 96 côtés ( le nombre de côtés est doublé à chaque fois
)
Nous utilisons ici la trigonométrie ; Archimède a utilisé
une méthode purement géométrique .
On
considère un polygone régulier à n côtés inscrit dans un cercle de rayon 1 .
Soit H pied de la hauteur issue de O dans le triangle OAB.
( Pour des raisons de commodités , c’est un hexagone
qui
Soit n le nombre de côtés du polygone ( n étant
égal à 6 ; 12 ; 24 ;
L’angle 
= 
radians
Le triangle AOB est isocèle en O donc l'angle
est égal à 
2 , soit 
Dans le triangle HOB rectangle en H , sin
= 
, soit sin = 
Donc AB = 2 
HB
= 2 sin
Le périmètre du polygone inscrit au cercle est
donc égal à 2 n sin
Dans le triangle HOB rectangle en H , tan
= 
,
soit =
HB = 2 tan
n tan
Finalement , si on appelle P le périmètre du cercle ,
P = 2 1
= 2
On a donc :
2 n tan < 2 <
2 n sin , soit n sin < < n tan
Remarque : il faudrait encore montrer
que les suites de terme général n sin et n tan convergent bien vers en utilisant le fait que
converge
vers en + 
et
que 
converge vers en + .
Pour n = 96 côtés ( valeur maximale d’Archimède ) :
3,141031951< < 3,142857
Pour n = 1536 côtés ( 96 2 2 2 2 ) : 3,141590463
< < 3,141597034
, et on trouve les
cinq premières décimales exactes .
Comment se souvenir des décimales de ?
Les chiffres de peuvent se retrouver
en comptant le nombre de lettres dans le texte ci-dessous :
« Que j’aime à faire apprendre un nombre utile aux sages !
3 1 4
1 5 9 2 6 5 3 5
Immortel Archimède
, artiste , ingénieux ,
8 9 7
9
Qui de ton jugement
peut priser ta valeur ?
3 2 3
8 4 6 2 5
Pour moi , ton problème eut de pareils avantages ! »
4 3
3 8 3 2 7 9
Depuis le XVIIIe siècle , les mathématiciens savent
que ne n’écrit pas à l’aide
d’une fraction .
Des valeurs exactes ou approchées de pi
v
Les babyloniens utilisaient 3 + 1/8 comme valeur approchée
de .
v
Les Egyptiens , au XVIIe siècle avant JC , utilisaient
3 + 
comme valeur approchée de .
v
En Inde , vers 380 avant JC , 3 + 
est
utilisé comme valeur approchée de .
+ 
comme valeur approchée de
v
En Chine , au Ve siècle , 
est
utilisé comme valeur approchée de .
v
Viète , au XVIe siècle , a trouvé que =
2 
v
Wallis , au XVIIe
siècle a trouvé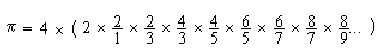 
ou encore
=
v
Leibniz , fin du XVIIe siècle , a trouvé 
;
formule la plus utilisée pour calculer les décimales de
v
Quelques fractions donnant une bonne approximation de :
La question est la suivante : construire un carré de surface égale à celle d'un disque de rayon fixé .
Si on prend 1
comme rayon du disque , l'aire est égale à . Il faut
donc trouver x le côté du carré tel que x² = .
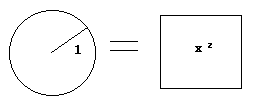
Ce problème
a été posé vers le 5e siècle avant JC ( peut-être
par Hippocrate de Chios ) , il fallait essayer de le résoudre à
la règle et au compas . Un tel problème a fait couler beaucoup
d'encre et n'a trouvé sa solution qu'en 1880 : Lindemann a montré
que est transcendant , c'est-à-dire
que
ne s'écrit pas sous la forme d'une racine ; une
telle démonstration fait appel à la théorie des nombres
. Ce résultat prouvait bien qu'une telle construction était
impossible . En effet , si
était un nombre
algébrique , il s'écrirait sous la forme d'une racine ,
et une racine
est constructible à la règle et au compas
( une racine
carrée est constructible à la règle et au compas
en utilisant des triangles rectangles )
Ce problème a laissé une trace derrière lui : l'expression " résoudre la quadrature du cercle" est devenue synonyme de réaliser l'impossible .
A voir
aussi un site très complet sur le nombre
: http://www.multimania.com/bgourevitch/
. Bon courage
!! )