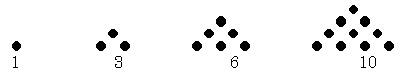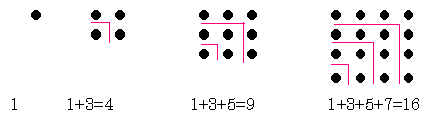
Qui
était Pythagore
Théorème de Pythagore
Triplets
pythagoriciens
Les
Pythagoriciens
Démonstration
du théorème :
par les chinois - par Garfield
- par la méthode des carrés - par
Euclide
construction
de la racine
réciproque du théorème
Qui
était Pythagore ?
Pythagore
était un mathématicien grec de la fin du 6e siècle avant JC
, il serait né au large des côtes de Turquie .
Il fonda l’école
des pythagoriciens qui était en fait une secte qui comptait environ 218 adeptes
. Elle dura environ 1500 ans . Ils avaient des activités religieuses , philosophiques , mathématiques et politiques
. La devise des pythagoriciens était «Toutes choses sont des nombres ».
Ceux qui étaient dans cette école rapportaient leurs découvertes scientifiques
à Pythagore. Il est donc impossible de distinguer les inventions de Pythagore
de celles de ses disciples.
Il
fut l’élève de Thalès
. Comme pour ce dernier , on ne dispose d’aucune œuvre car à cette époque
l’enseignement était oral. On ne sait donc pas si Pythagore a démontré son
propre théorème.
La mort
de Pythagore semble étrange . Voici la version la plus répandue
: un jour , sa maison fut incendiée par ses ennemis .Plusieurs de ses
disciples furent tués . Pythagore lui-même se sauva pour se retrouver
dans un champ de haricots . Il s'arrêta et déclara qu'il préférait
être tué plutôt que de traverser ce champ de haricots .
Ses poursuivants le prirent au mot et lui tranchèrent la gorge .

Théorème
de Pythagore
 Le
théorème de Pythagore était connu des Babyloniens
( soit 100 ans avant Pythagore ) : des textes gravés sur une tablette
d’argile ont été trouvés . Précisons que les Babyloniens ne connaissaient
pas le théorème sous sa forme générale mais utilisaient
ce qu'on appelle des triplets pythagoriciens .
Le
théorème de Pythagore était connu des Babyloniens
( soit 100 ans avant Pythagore ) : des textes gravés sur une tablette
d’argile ont été trouvés . Précisons que les Babyloniens ne connaissaient
pas le théorème sous sa forme générale mais utilisaient
ce qu'on appelle des triplets pythagoriciens .
 Rappelons
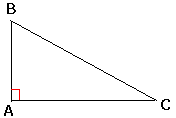
son énoncé : «Dans un triangle rectangle , le carré de l’hypoténuse
est égal à la somme des carrés des deux autres côtés » . Soit :
si ABC est un triangle rectangle en A , on a : BC ² = AB ² + AC ²
Rappelons
son énoncé : «Dans un triangle rectangle , le carré de l’hypoténuse
est égal à la somme des carrés des deux autres côtés » . Soit :
si ABC est un triangle rectangle en A , on a : BC ² = AB ² + AC ²
 Ce
fameux « théorème de Pythagore » ( appelé ainsi depuis le milieu
du XXe siècle)fut appelé au début du XXe siècle « le
Pont-aux-ânes de la géométrie » par les lycéens.( connaissance permettant
de juger de l’intelligence de quelqu’un). Il a eu , au fil du temps différents
noms : « Théorème de la mariée » chez les Grecs ;
« Chaise de la mariée » chez les Hindous , « Figure de l'épousée
» chez les Perses pour la réciproque du théorème de Pythagore.
Ce
fameux « théorème de Pythagore » ( appelé ainsi depuis le milieu
du XXe siècle)fut appelé au début du XXe siècle « le
Pont-aux-ânes de la géométrie » par les lycéens.( connaissance permettant
de juger de l’intelligence de quelqu’un). Il a eu , au fil du temps différents
noms : « Théorème de la mariée » chez les Grecs ;
« Chaise de la mariée » chez les Hindous , « Figure de l'épousée
» chez les Perses pour la réciproque du théorème de Pythagore.
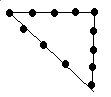
 En
Mésopotamie , en Inde, et même en Egypte , on utilisait des cordes à nœuds
pour obtenir des angles droits ( pour construire des autels ...)( par
exemple une corde à 13 nœuds régulièrement espacés permet de tracer un triangle
de côtés 3 ; 4 ; 5
En
Mésopotamie , en Inde, et même en Egypte , on utilisait des cordes à nœuds
pour obtenir des angles droits ( pour construire des autels ...)( par
exemple une corde à 13 nœuds régulièrement espacés permet de tracer un triangle
de côtés 3 ; 4 ; 5
( les nœuds
n°1 et 13 se confondent )

Triplets
pythagoriciens
 Voici
une liste de nombres vérifiant la relation de Pythagore a²+b²=c² ( un triangle dont les côtés mesurent les longueurs suivantes
est rectangle ) :
Voici
une liste de nombres vérifiant la relation de Pythagore a²+b²=c² ( un triangle dont les côtés mesurent les longueurs suivantes
est rectangle ) :
( 3 ;
4 ; 5 ) ( 5 ; 12 ;
13 ) ( 6 ; 8 ; 10 )
( 7 ; 24 ; 25 ) (
8 ; 15 ; 17 ) (12 ;
16 ; 20 )
(12 ; 35 ; 37 ) (
15 ; 20 ; 25 ) ( 15 ;
36 ; 39 ) ( 20 ; 21 ;
29 ) ( 119 ; 120 ;
169 )
Les
triplets sont connus des maçons qui les utilisent pour « fabriquer »
des angles droits.
Ces triplets
de nombres sont appelés triplets
pythagoriciens car ils peuvent être la mesure des trois côtés d’un triangle
rectangle .


Tablette conservée à l'université
de Columbia à New-York ; elle est composée de 4 colonnes et
15 rangées de nombres , elle appartiendrait à une tablette plus
grande qui aurait été brisée ; on pense qu'elle donne
une procédure de triplets pythagoriciens fractionnaires .
Ceci prouve que les Babyloniens connaissaient
le théorème de Pythagore dès 1800 - 1650 avant JC , soit
un millier d'années avant Pythagore !
 Pour
trouver de tels triplets , on écrit : a = k ( m² + n² ) b = k ( m² - n² ) c = 2 k m n
Pour
trouver de tels triplets , on écrit : a = k ( m² + n² ) b = k ( m² - n² ) c = 2 k m n
Où k , m et n sont trois nombre entiers
; m> n et m et n de parités différentes
On
peut aussi obtenir de tels triplets ainsi : soit n un nombre entier quelconque.
a = 2 n + 1 b = 2 n ² + 2 n c = 2 n ² + 2 n + 1
Quelques triplets pythagoriciens

Les
Pythagoriciens
Ils ont découvert :
 Ils construisent trois polyèdres
réguliers ( parmi les cinq ) : le cube , le tétraèdre et le dodécaèdre . Platon avait démontré
qu’il n’existait que cinq polyèdres réguliers dans l’espace , les deux autres
étant l’icosaèdre et l’octaèdre.( Un polyèdre régulier est un solide ayant
toutes ses faces qui sont des polygones réguliers ( carré , triangle équilatéral
, pentagone régulier…) )
Ils construisent trois polyèdres
réguliers ( parmi les cinq ) : le cube , le tétraèdre et le dodécaèdre . Platon avait démontré
qu’il n’existait que cinq polyèdres réguliers dans l’espace , les deux autres
étant l’icosaèdre et l’octaèdre.( Un polyèdre régulier est un solide ayant
toutes ses faces qui sont des polygones réguliers ( carré , triangle équilatéral
, pentagone régulier…) )
 Ils ont défini les nombres triangulaires
, carrés , pentagonaux
Ils ont défini les nombres triangulaires
, carrés , pentagonaux
 Les nombres
triangulaires :
Les nombres
triangulaires :
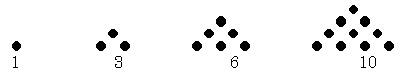
 Les nombres carrés :
Les nombres carrés :
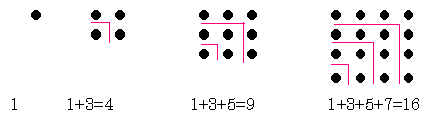
Ils
ont ainsi trouvé comment calculer la somme des n premiers nombres impairs
( égal à n² )
 Les nombres
pentagonaux :
Les nombres
pentagonaux :

Démonstration
par les Chinois
Le
théorème de Pythagore a été démontré par Euclide.
Il existe environ
367 démonstrations de ce théorème. La plus ancienne est une démonstration
chinoise.
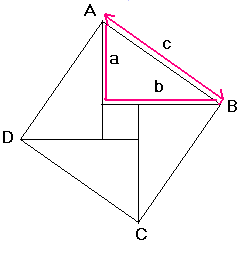
On
démontre d’abord que ABCD est un carré . Puis ,on calcule l’aire du carré
ABCD de deux façons :
aire
= c  c
= c²
c
= c²
aire = 4  aire
du triangle + aire du petit carré de côté (b-a)
aire
du triangle + aire du petit carré de côté (b-a)
= 4 [(a b)
b) 2] + ( b – a )²
2] + ( b – a )²
= 2ab + a² + b² - 2 ab
= a² + b²
Finalement , on obtient bien a²+b² = c²

Démonstration
par Garfield en 1876
Garfield a été le 20e président des Etats-Unis ; il s’est inspiré
de la démonstration des Chinois.
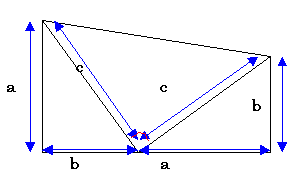
On se donne deux triangles rectangles de côtés a ; b et c disposés comme l’indique la figure ci-dessus :
On calcule l’aire du trapèze ainsi formé :
A = [( b + a )  (a+b)]
(a+b)]  2 = ( a² + 2ab + b² )
2 = ( a² + 2ab + b² )  2 = (a²
2 = (a²  2) + ab + (b²
2) + ab + (b² 2)
2)
D’autre part , l’aire de ce trapèze est égale à la somme des aires
des trois triangles rectangles ( il faudrait encore démontrer que le 3e triangle
est bien rectangle en utilisant le fait que les deux angles d’un triangle
rectangle autre que l’angle droit sont complémentaires ) :
A = (ab  2 ) + (ab
2 ) + (ab  2 ) + (c²
2 ) + (c²  2)= ab + (c²
2)= ab + (c²  2)
2)
En égalant les deux résultats trouvés , on peut écrire :
(a²
 2) + ab + (b²
2) + ab + (b² 2) = ab + (c²
2) = ab + (c²  2) soit : (a²
2) soit : (a²  2)
+ (b²
2)
+ (b² 2) =c²
2) =c²  2
2
On obtient donc bien : a²+b² = c²

Autre
démonstration du théorème de Pythagore

On dispose
de quatre triangles rectangles d’hypoténuse a et de côtés b et c .
On
démontre d’abord que JGHI est un carré ( on utilise le fait que les deux angles
, autres que l’angle droit , sont complémentaires )
On
calcule dans les deux figures les aires en blanc qui sont égales :
Par le premier
dessin , aire de JGHI = a²
Par le deuxième
dessin , aire = aire du carré VNUW + aire du carré TWSQ = c² + b²
D’où : a² = b² + c ²

Démonstration
par Euclide
On
se donne un triangle ABC rectangle en A . On veut prouver que AB² + AC² =
BC²
On construit les trois carrés
à l’extérieur du triangle de côtés respectifs AB ; AC et BC .

Les deux triangles FBC et ABD ont deux côtés égaux ( AB = BF et BC
= BD ) et un angle égal (FBC = ABD ) ; ils sont donc identiques .
Aire de ABD = BD  BI
BI  2 et aire de BILD = BD
2 et aire de BILD = BD  BI donc aire de BILD = 2
BI donc aire de BILD = 2  Aire de ABD
Aire de ABD
De même , aire de BFGA = 2  Aire de FBC
Aire de FBC
Finalement , les triangles FBC et ABD étant identiques , on en déduit
que : aire de BILD = aire de BFGA
De même , on montre que : aire de CILE = aire de ACKH
Or , aire de BCED = aire de BILD + aire de CILE
Donc : aire de BCED = aire
de BFGA + aire de ACKH C’est-à-dire : BC² =
AB² + BC²

Construction
de la racine carrée d'un nombre de façon exacte
On part d’un triangle rectangle ayant pour côtés de l’angle droit
1 cm et 1 cm .
On construit alors le 3e côté
du triangle rectangle de longueur  cm.
cm.
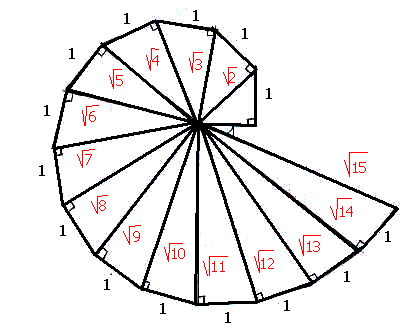
En suivant la construction indiquée ci-dessus , on construit des
segments de longueurs successivement égales à 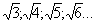 cm .
cm .

Réciproque
du théorème de Pythagore
Rappelons
son énoncé : «Si dans un triangle , le carré de l’hypoténuse est égal
à la somme des carrés des deux autres côtés , alors ce triangle est rectangle »
. Soit : si dans un triangle BC ² = AB ² + AC ² , alors ce triangle est
rectangle en A .
Voir
la démonstration

![]() Le
théorème de Pythagore était connu des Babyloniens
( soit 100 ans avant Pythagore ) : des textes gravés sur une tablette
d’argile ont été trouvés . Précisons que les Babyloniens ne connaissaient
pas le théorème sous sa forme générale mais utilisaient
ce qu'on appelle des triplets pythagoriciens
Le
théorème de Pythagore était connu des Babyloniens
( soit 100 ans avant Pythagore ) : des textes gravés sur une tablette
d’argile ont été trouvés . Précisons que les Babyloniens ne connaissaient
pas le théorème sous sa forme générale mais utilisaient
ce qu'on appelle des triplets pythagoriciens ![]() Rappelons
son énoncé : «Dans un triangle rectangle , le carré de l’hypoténuse
est égal à la somme des carrés des deux autres côtés » . Soit :
si ABC est un triangle rectangle en A , on a : BC ² = AB ² + AC ²
Rappelons
son énoncé : «Dans un triangle rectangle , le carré de l’hypoténuse
est égal à la somme des carrés des deux autres côtés » . Soit :
si ABC est un triangle rectangle en A , on a : BC ² = AB ² + AC ² 
![]() Ce
fameux « théorème de Pythagore » ( appelé ainsi depuis le milieu
du XXe siècle)fut appelé au début du XXe siècle « le
Pont-aux-ânes de la géométrie » par les lycéens.( connaissance permettant
de juger de l’intelligence de quelqu’un). Il a eu , au fil du temps différents
noms : « Théorème de la mariée » chez les Grecs ;
« Chaise de la mariée » chez les Hindous , « Figure de l'épousée
» chez les Perses pour la réciproque du théorème de Pythagore.
Ce
fameux « théorème de Pythagore » ( appelé ainsi depuis le milieu
du XXe siècle)fut appelé au début du XXe siècle « le
Pont-aux-ânes de la géométrie » par les lycéens.( connaissance permettant
de juger de l’intelligence de quelqu’un). Il a eu , au fil du temps différents
noms : « Théorème de la mariée » chez les Grecs ;
« Chaise de la mariée » chez les Hindous , « Figure de l'épousée
» chez les Perses pour la réciproque du théorème de Pythagore.![]() En
Mésopotamie , en Inde, et même en Egypte , on utilisait des cordes à nœuds
pour obtenir des angles droits ( pour construire des autels ...)( par
exemple une corde à 13 nœuds régulièrement espacés permet de tracer un triangle
de côtés 3 ; 4 ; 5
En
Mésopotamie , en Inde, et même en Egypte , on utilisait des cordes à nœuds
pour obtenir des angles droits ( pour construire des autels ...)( par
exemple une corde à 13 nœuds régulièrement espacés permet de tracer un triangle
de côtés 3 ; 4 ; 5![]() Voici
une liste de nombres vérifiant la relation de Pythagore a²+b²=c² ( un triangle dont les côtés mesurent les longueurs suivantes
est rectangle ) :
Voici
une liste de nombres vérifiant la relation de Pythagore a²+b²=c² ( un triangle dont les côtés mesurent les longueurs suivantes
est rectangle ) : ![]()

![]()