Enoncé de la réciproque du théorème de Pythagore :

«Si ABC est un triangle vérifiant AB² + AC² = BC² , alors ABC est un triangle restangle en A ».

Les données et ce qu'on doit démontrer

Soit ABC un triangle quelconque vérifiant AB² + AC² = BC² ; et soit H le pied de la hauteur issue de C .

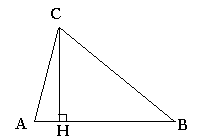
Pour montrer que ABC est un triangle rectangle en A , il suffit de montrer que le point C est confondu avec H

Démonstration

• Dans le triangle ACH rectangle en H , AH² + CH² = AC² (1) d'après le théorème de Pythagore
• Dans le triangle CBH rectangle en H , CH² + BH² = BC² (2) d'après le théorème de Pythagore

• AB² + AC² = AB² + ( AH² + CH² ) d'une part en utilisant (1) ,
• BC² = CH² + BH² d'autre part en utilisant (2).

• Comme AB² + AC² = BC² par hypothèse , on en déduit que :
• AB² + ( AH² + CH² ) = CH² + BH² ; soit AB² + AH² = BH² (*)

1er cas : H appartient à [AB] , mais H est différent de A

On a donc AB = AH + HB ; soit en élevant les deux membres au carré : AB² = AH² + HB² + 2 AH . HB

(*) devient : AH² + HB² + 2 AH . HB + AH² = BH²; soit en simplifiant AH² + AH.HB= 0

Or , H étant différent de A , AH>0 et donc AH² + AH.HB > 0 et est donc différent de zéro .

Donc le point H n'appartient pas à [AB]

2e cas : H appartient à [BA) , mais pas à [AB]

Le point A appartient donc à [BH] , donc BH = BA + AH

Soit en élevant les deux membres au carré : HB² = AB² + AH² + 2 AB . AH

(*) devient : AB² + AH² = AB² + AH² + 2 AB . AH ; soit en simplifiant AB . AH = 0

Comme AB > 0 et AH > 0 ( H n'est pas sur le segment [AB] ) , AB . AH > 0

Donc le point H n'appartient pas à [BA)

3e cas : H appartient à [AB) , mais pas à [AB]

Le point B appartient donc à [AH] , donc AH = AB + BH

Soit en élevant les deux membres au carré : AH² = AB² + HB²+ 2 AB . BH

Comme AB² + AH² = BH² ; (*) devient : AB² + AB² + HB²+ 2 AB . BH= BH² ;

soit en simplifiant AB² + AB . BH = 0

Comme AB > 0 et BH > 0 ( H n'est pas sur le segment [AB] ) , AB . BH > 0

Donc le point H n'appartient pas à [AB)

4e cas : H et A sont confondus

(*) devient : AB² + AA² = BA² ; aucune contradiction .

Conclusion :

A et H sont confondus . Comme (HC) est perpendiculaire à (HB) ; (AC) est perpendiculaire à (AB); ABC est donc bien un triangle rectangle en A .