
Thalès était
un mathématicien grec qui aurait vécu au 6e siècle avant JC. Il
était aussi commerçant , astronome , ingénieur
et philosophe .
Il n'existe
aucune certitude historique sur la vie de Thalès . Seuls quelques textes
grecs permettent de retracer sa vie.
On lui attribue
de nombreuses propriétés :
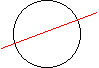
![]() « Un
cercle est symétrique par rapport à ses diamètres »
« Un
cercle est symétrique par rapport à ses diamètres »
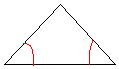
![]() « Un triangle isocèle a les deux angles
à la base égaux »
« Un triangle isocèle a les deux angles
à la base égaux »
![]() « Deux angles opposés par le sommet ont
la même mesure »
« Deux angles opposés par le sommet ont
la même mesure »

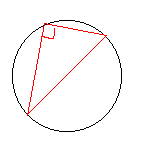
![]() « Si un triangle est inscrit dans un cercle
de diamètre un côté du triangle , alors ce triangle est rectangle »
« Si un triangle est inscrit dans un cercle
de diamètre un côté du triangle , alors ce triangle est rectangle »
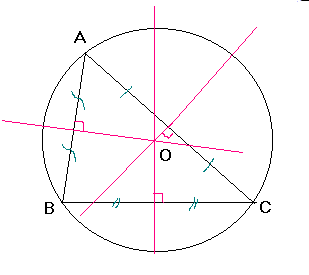
![]() Il
a démontré aussi qu’à chaque triangle , on peut faire correspondre un cercle
, le cercle circonscrit au triangle . Il a proposé une construction générale
de ce cercle .
Il
a démontré aussi qu’à chaque triangle , on peut faire correspondre un cercle
, le cercle circonscrit au triangle . Il a proposé une construction générale
de ce cercle .
Il fut le premier
à considérer l’angle comme la quatrième grandeur géométrique ( les trois autres
étant la longueur , la surface et le volume)
Le fameux théorème
de Thalès aurait été trouvé en voulant mesurer la hauteur d’une pyramide en
Egypte. Pour cela il aurait utilisé un bâton , l’ombre de ce bâton et l’ombre
de la pyramide.
Il a choisi le moment où les rayons solaires étaient perpendiculaires à une face latérale ( ce qui était possible car les pyramides avaient une face plein sud ! ) et tel que son ombre soit égale à sa taille ( donc les rayons du soleil étaient inclinés de 45° ). Ce moment bien spécifique est possible 2 fois par an !
Le rapport
entre sa taille et son ombre est donc égal au rapport entre la hauteur de
la pyramide et la longueur de son ombre.
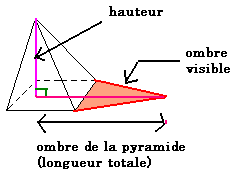
Pour effectuer
les mesures, il aurait tracé dans le sable un cercle de rayon égal à sa taille
, et plaça un bâton au centre de même taille que lui ; puis quand l’ombre
du bâton toucha le cercle, il planta un autre bâton pour indiquer l’extrémité
de l’ombre de la pyramide .
( Les pyramides
ont une base carrée)
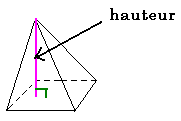
La hauteur de la pyramide de Khéops est donc égale à 85 Thalès . En mesure locale, 1 Thalès équivaut environ à 3,25 coudées égyptiennes donc 85 Thalès équivalent à 280 coudées soit environ 147 m . Il avait donc pris un cas particulier du théorème que nous connaissons aujourd’hui, celui où le rapport entre la hauteur de la pyramide et son ombre est égal à 1.
« Si
on mène une droite parallèle à un des côtés
du triangle , cette droite coupera proportionnellement les côtés de
ce triangle ; et si les côtés d’un triangle sont coupés proportionnellement
, la droite qui joindra les sections sera parallèle au côté restant du triangle »
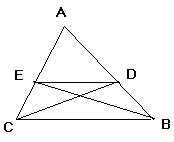
Il faut montrer
que ![]()
On se donne
(ED) // (BC)
Aire BDE =
aire CDE donc ![]()
Or , BDE et
AED ont une hauteur commune : c’est la hauteur issue de E dans les deux
triangles .
Aire BDE =
h ![]() DB
DB
![]() 2 et aire AED = h
2 et aire AED = h ![]() AD
AD
![]() 2 donc
2 donc ![]()
Or , CDE et
AED ont une hauteur commune : c’est la hauteur issue de D dans les deux
triangles .
Aire CDE =
h ![]() CE
CE
![]() 2 et aire AED = h
2 et aire AED = h ![]() AE
AE
![]() 2 donc
2 donc ![]()
Donc :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()