Accès rapide :   

Livre 1    Livre 2     Livres 3/4/5     Livres 6 /7/8/9   Livres 10/11/12/13

Qui était Euclide ?

C’était un mathématicien grec qui aurait vécu au IIIe siècle avant JC, peu avant Archimède . On ne sait rien de précis sur sa vie. Il a posé les fondements de la géométrie dans son livre « Eléments » , dans lequel il écrit 465 propositions .

Les « Eléments »  sont constitués de treize livres ; on ignore cependant s’ils ont été écrits par Euclide seulement . Dans « Eléments », il n’aborde que des problèmes dont les solutions se construisent à la règle et au compas.

Il était l'un des premiers mathématiciens de l'école d'Alexandrie , qui dura de 323 avant JC à 640 .Cette école fut fondée sous le règne d'Alexandre le Grand , par Straton , élève d'Aristote.Dans cette école on y retrouve Aristarque , Apollonius , Eratosthène ...

"Eléments" d'Euclide

Les quatre premiers livres traitent de la géométrie plane , propriétés des figures rectilignes et des cercles. Dans ces quatre livres , il identifie les figures , il calcule leur aire ( sauf celle du cercle ) et procède à leur construction.

 Le livre I  :

  Il donne les définitions de base de la géométrie : 

Définition 1 : « Le point est ce dont la partie est nulle » .

Définition 2 : « Une ligne est une longueur sans largeur ».

Définition 3 : « Les extrémités d’une ligne sont des points. »

Définition 4 :  « La ligne droite est celle qui est également placée entre ses points »

Définition 5 : « Une surface est ce qui a seulement longueur  et largeur » .

Définition 6 : « Les extrémités d’une surface sont des lignes. »

Définition 7 : « La surface plane est celle qui est également placée entre ses droites ». 

Définition 8 : « Un angle plan est l’inclinaison mutuelle de deux lignes qui se touchent dans un plan , et qui ne sont point placées dans la même direction »

Définition 9 : « Lorsque les lignes , qui comprennent ledit angle , sont des droites , l’angle se nomme  rectiligne »

Définition 10 : « Lorsqu’une droite tombant sur une droite fait deux angles de suite égaux entre eux , chacun des angles égaux est droit ; et la droite placée au-dessus est dite perpendiculaire à celle sur laquelle elle est placée ».

Définition 11 : « L’angle obtus est celui qui est plus grand qu’un angle doit »

Définition 12 : « L’angle aigu est celui qui est plus petit qu’un angle doit »

Définition 13 : « On appelle limite ce qui est l’extrémité de quelque chose »

Définition 14 : « Une figure est ce qui est compris par une seule ou par plusieurs limites »

Définition 15 : « Un cercle est une figure plane , comprise par une seule ligne qu’on nomme circonférence ; toutes les droites , menées à la circonférence d’un de ses points placées dans cette figure , étant égales entre elles ».

Définition 16 : « Ce point se nomme centre du cercle »

Définition 17 : « Le diamètre du cercle est une droite menée par le centre , et terminée de part et d’autre par la circonférence du cercle : le diamètre partage le cercle en deux parties égales ».

Définition 18 : « Un demi-cercle est la figure comprise par le diamètre , et la portion de la circonférence , soutendue par le diamètre »

Définition 19 : « Un segment de corde est la figure comprise par une droite et par la circonférence du cercle ; le demi-cercle étant plus grand ou plus petit que le segment ».

Définition 25 : «Le triangle isocèle , celle qui a seulement deux côtés égaux »

Définition 26 : «Le triangle scalène , celle qui a trois côtés inégaux »

Définition 27 : «De plus , parmi les figures trilatères , le triangle rectangle est celle qui a un angle droit »

Définition 28 : «Le triangle obtusangle , celle qui a un angle obtus »

Définition 29 : «Le triangle acutangle , celle qui a ses trois angles aigus »

Définition 30 : «Parmi les figures quadrilatères , la quarré est celle qui est équilatérale et rectangulaire »

Définition 31 : «Le rectangle , celle qui est rectangulaire , et non équilatérale »

Définition 32 : «Le rhombe , celle qui est équilatérale , et non rectangulaire »

Définition 33 : «Le rhomboïde , celle qui a ses côtés et ses angles opposés égaux entre eux , et qui n’est ni équilatérale ni rectangulaire »

Définition 34 : «Les autres quadrilatères , ceux-là exceptés , se nomment trapèzes ».

Définition 35 : «Les parallèles sont des droites , qui , étant situées dans un même plan , et étant prolongées à l’infini de part et d’autre , ne se rencontrent ni d’un côté ni de l’autre ».

Il écrit ensuite cinq postulats :

( un postulat est une phrase qu’on demande d’admettre , étant considérée comme évidente , et n’ayant par conséquent pas besoin d’être démontrée ) : ( écrit en langage moderne ) 

Postulat 1 : Par deux points distincts , il passe une droite et une seule .

Postulat 2  :Tout segment [AB] est prolongeable en une droite passant par A et B

Postulat 3 : Par deux points distincts A et B , on peut décrire un cercle de centre A et passant par B

Postulat 4 : « Tous les angles droits sont égaux entre eux ».

Postulat 5 : ( appelé postulat d’Euclide), Par un point extérieur à une droite , il passe une droite et une seule parallèle à la  droite donnée.

Postulat 6 : « Deux droites ne renferment point un espace ».

Bien des mathématiciens ont cherché à démontrer le 5e postulat à partir des quatre autres ! Mais ce n'est pas si facile !

Il écrit ensuite des axiomes ( ou notions communes) :

Un axiome est de nature évidente. axiome vient du grec axioma qui signifie « j’estime , je crois vrai » , ce qui conduit au sens «  irréfutable , évident ».

Axiome 1 : « Les grandeurs égales à une même grandeur , sont égales entre elles ».

Axiome 2 : « Si à des grandeurs égales , on ajoute des grandeurs égales , les touts seront égaux».

Axiome 3 : « Si de grandeurs égales , on retranche des grandeurs égales , les restes seront égaux »

Axiome 4 : « Si à des grandeurs inégales , on ajoute des grandeurs égales , les touts seront inégaux».

Axiome 5 : « Si de grandeurs inégales , on retranche des grandeurs égales , les restes seront inégaux »

Axiome 6 : « Les grandeurs , qui sont doubles d’une même grandeur , sont égales entre elles »

Axiome 7 : « Les grandeurs , qui sont les moitiés d’une même grandeurs , sont égales entre elles »

Axiome 8 : « Les grandeurs , qui s’adaptent entre elles , sont égales entre elles ».

Axiome 9 : « Le tout est plus grand que la partie ».

*  Le livre II :

Il pose les fondements de l’algèbre géométrique . Des segments de droites remplacent des nombres.

Par exemple :

a . b       désigne l’aire du rectangle de côtés a et b.

a . b . c  désigne le volume  d’un pavé de côtés a ; b et  c.

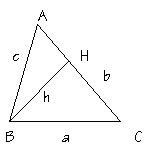
Il écrit dans ce livre et démontre ce qu’on pourrait appeler le théorème de Pythagore généralisé dans un triangle quelconque :

ABC est un triangle quelconque . On pose AB = c ; AC = b et BC = a

Alors : BC² = AB² + AC² - 2 AC AH ou encore : BC² = AB² + AC² - 2 AB AC cos A  

*  Le livre III :

Livre sur la géométrie du cercle.Il étudie la puissance d'un point par rapport à un cercle ainsi que la notion de tangente.

* Le livre IV :

Livre sur la géométrie du compas.

Il construit les polygones réguliers ( polygone qui a tous ses côtés de même longueur)

Pour chacun d’eux , il détermine le cercle inscrit et le cercle circonscrit.

*  Le livre V :

Livre difficile sur la théorie des proportions.

Il établit ce qu’est un rapport entre deux grandeurs , que ces nombres soient géométriques ( lignes , surfaces , volumes ) ou arithmétiques ( nombres ) . Il donne 18 définitions et 25 théorèmes .

Définition 3 : " Un rapport est une certaine manière d'être de deux grandeurs homogènes entre elles , suivant la quantité " .

Définition 4 : " Des grandeurs sont dites avoir un raport entre elles , lorsque ces grandeurs , étant multipliées , peuvent se surpasser mutuellement " .

Définition 5 : " Des grandeurs sont dites être dans un même rapport , la première à la deuxième et la troisième à la quatrième , lorsque des équimultiples quelconques de la première et de la troisième et d'autres équimultiples quelconques de la seconde à la quatrième , sont tels que les premiers équimultiples surpassent , chacun à chacun , les seconds équimultiples ou leur sont égaux à la fois , ou plus petits à la fois " .

Définition 6 : " Les grandeurs qui ont le même rapport sont dites proportionnelles "

Définition 7 : " Lorque , parmi ces équimultiples , un multiple de la première surpasse un multiple de la seconde , et qu'un multiple de la troiqième ne surpasse pas un multiple de la quatrième , on dit alors que la première a , avec la seconde , un plus grand rapport que la troiqième à la quatrième . "

Il énonce ensuite 25 propositions .

 

*  Le livre VI :

Application de la théorie des proportions aux aires.

Deux figures sont semblables quand elles sont proportionnelles . Elles sont proportionnelles si leurs côtés correspondants sont proportionnels et si leurs angles correspondants sont égaux .Il étudie le cas des similitudes de triangles .

«  Les triangles et les parallélogrammes  qui ont la même hauteur sont comme leurs bases ».

Il démontre le théorème de Thalès dans la proposition 2 .

Il introduit les angles inscrits et angles au centre.

*  Les livres VII , VIII et IX :

Théorie des proportions appliquées aux nombres : parité , divisibilité , existence d’une infinité de nombres premiers … Il reprend une grande partie des travaux pythagoriciens sur les nombres entiers.

Il parle aussi de PPCM , PGCD de deux nombres  , de décomposition en facteurs premiers .

Il prouve que tout nombre entier supérieur à 1 , est soit premier , soit il est le produit de nombres premiers ,et ce de façon unique . Il montre aussi que la liste des nombres premiers est infinie .

*  Le livre X :

C ‘est le livre le plus difficile à lire .

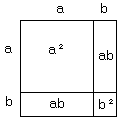
Classification des quantités irrationnelles qui y sont représentées géométriquement par des droites et des rectangles. Il démontre géométriquement des égalités  que nous écrivons aujourd’hui :

    et

On retrouve dans ce livre ce que nous appelons les identités remarquables : " Si une droite est coupée à volonté , le carré de la droite entière est égal aux carrés des segments et à deux fois le rectangle contenu sous les deux segments " ; mieux connu sous la forme notée aujourd'hui : ( a + b ) ² = a ² + 2ab + b ² .

Il étudie les longueurs qui se déduisent d'une longueur de base au moyen de construction à la règle et au compas . Il démontre aussi l'irrationnalité du rapport de la diagonale du carré à son côté .

Proposition 1 : " Deux grandeurs inégales étant données , si l'on retranche de la plus grande une partie plus grande que sa moitié , si l'on retranche du reste une partie plus grande que sa moitié , et si l'on fait toujours la même chose , il restera une certaine grandeur qui sera plus petite que la plus peite des grandeurs proposées" .

Les propositions 1 ; 2 et 3 concernent l'algorithme d'Euclide appliqué .

* Le livre XI :

Géométrie dans l’espace.

Les 19 premières propositions sont sur les droites et plans parallèles ou perpendiculaires . Il écrit quatre énoncés relatifs aux angles trièdres appelés " angles solides compris sous trois angles plans " . De la 20e à la 40e proposition , il traite des volumes des pavés et des prismes .

proposition 32 : " Les parallélépipèdes qui ont la même hauteur sont entre eux comme leurs bases ."

*  Le livre XII :

Il compare les aires curvilignes à celles des aires des polygones. Il traite des solides : pyramide , prisme , cône , cylindre , sphère , polyèdres réguliers . Il calcule les aires et les volumes de certains , détermine les rapports entre volumes pour d’autres.

" Les cercles sont entre eux comme les carrés de leurs diamètres".

La proposition 9 concerne le volume de la pyramide .

Les propositions 10 à 15 concernent les volumes du cylindre droit et du cône de révolution .

Les propositions 16 à 18 concernent le volumes de la sphère."Les sphères sont entre elles en raison triplées de leurs diamètres" ( c'est-à-dire leurs volumes sont proportionnels aux cubes de leurs diamètres"

*  Le livre XIII :

C’est un résumé des douze autres.

Construction des 5 polyèdres réguliers convexes inscrits dans la sphère.