Archimède,
fils de l’astronome Phidias ( ce dernier a déterminé que le
périmètre du Soleil est douze fois plus grand que celui de la
Terre ) , est un Grec né à Syracuse, en 287 avant JC.
Celui qui nous permet de retrouver sa date de naissance est le poète du XIIe siècle Tzetzès qui nous dit qu'Archimède a vécu jusqu'à l'âge de 75 ans ; comme la date de sa mort nous est connue avec certitude , on en déduit donc l'année de sa naissance .
Tous les portraits le représentent sous la forme d'un vieillard barbu ou sous les traits d'un homme plus jeune courant dans les rues .
Statue du National Museum de Naples
La
légende raconte que lorsque les troupes du consul romain Marcellus
( homme politique et général romain ) envahirent Syracuse ,
il était occupé à résoudre un problème
de géométrie .Un soldat romain entra dans sa maison , lui demandant
de le suivre ; mais Archimède lui ordonna d'attendre qu'il eût
fini de résoudre son problème .Le soldat le transperça
alors d'un coup de glaive ( alors que Marcellus avait demandé qu’on l’épargnât
) en 212 avant JC.
Il
passa sa vie à Syracuse en Sicile . Issu d'une famille aisée
,sans être très riche , il a pu se consacrer à la science
sans avoir à travailler pour subvenir à ses besoins .
Formé
en Égypte, par des élèves de l’école Euclidienne, il a intégré puis dépassé les principes d’Euclide
Qu'a-t-il
trouvé en tant que mathématicien ?
Il
mit au point une méthode pour calculer une bonne
approximation du nombre pi.
Il faut cependant noter que pour Archimède , le nombre pi n'avait pas le statut de nombre , c'était seulement le rapport entre le périmètre du cercle et le diamètre.
Il
a montré que la surface
d'une sphère est quatre fois celle de son grand cercle
.
Il a montré qu'une sphère inscrite dans un cylindre occupe les deux-tiers de son volume .
Il a montré que la surface de la sphère est égale aux deux-tiers de celle du cylindre.
Selon lui , c'est Eudoxe de Cnide qui a le premier montré que le volume d'un cône est égal au tiers du volume d'un cylindre de même base et de même hauteur .
Il
démontre trois propriétés importantes dans " La
mesure du cercle " :
"Tout
cercle est équivalent à un triangle dont la hauteur et la base
sont le rayon et la circonférence."
"
le rapport du cercle au carré circonscrit est proche de celui de 11
à 14 " .
"
Le périmètre de tout cercle est égal au triple du diamètre
augmenté d'un segment compris entre les dix soixante et onzièmes
et le septième du diamètre " . ( Il fixe 
comme valeur approchée de 
)
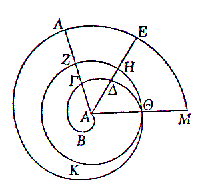
la
spirale d'Archimède
: Prenons un grand plateau circulaire qui tourne autour de son centre à
vitesse constante.On y place dessus une feuille de papier .A la verticale
du centre , on y plante une tige de métal.On fixe un rail électrique
horizontal où on y accroche un crayon à la verticale . La pointe
du crayon frôle le plateau et se déplace du centre vers l'extérieur
du plateau à vitesse constante. La courbe obtenue sur la feuille est
la spirale d'Archimède .
Mathématiquement
, elle est définie comme le lieu géométrique d'un point
M qui parcourt une demi-droite avec une vitesse constante , elle-même
à vitesse anguliare constante. Elle a pour équation polaire
: r = a
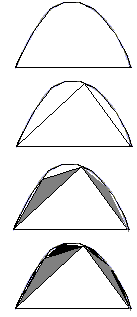
La
parabole : Il a mesuré la surface de la parabole en utilisant la
notion d'infini . Il inscrivit un triangle dans la parabole. Dans les deux
petits espaces restants , il inscrivit deux autres triangles .Il restait quatre
trous à combler avec d'autres triangles ....Les surfaces des triangles
s'approchaient vite de zéro.Archimède fit la somme des surfaces
de l'infinité des triangles et trouva la surface de la parabole .
Qu'a-t-il
trouvé en tant que physicien?
"La
poussée d'Archimède": Tout corps plongé dans un
liquide subit de la part de celui-ci , une poussée exercée du
bas vers le haut , et égale , en intensité , au poids du liquide
déplacé" .
Le
roi Hiéron avait un diadème mais il n‘était pas sûr que le bijoutier
n’avait pas travaillé avec d’autres matériaux que de l’or pur. Il demanda
donc à Archimède de s'en assurer sans détruire sa couronne.
Ce dernier, lors d’un bain , prend conscience de la poussée de l’eau en fonction
de la densité des matériaux et concrétise une méthode pour rassurer Hiéron.
(
La légende dit qu’il serait sorti de l’eau tout nu en criant : « eurêka »,(
j’ai trouvé ! ) et qu'il aurait traversé la ville en oubliant
de s'habiller pour faire part de sa découverte au roi .)
Les
corps flottants
:un objet plongé dans un liquide a tendance à s'enfoncer sous
l'effet de son poids ; mais le liquide résiste en poussant l'objet
vers le haut .Pour savoir si un objet flotte ou coule , il faut comparer le
poids de l'objet et la poussée opposée par le liquide. Archimède
a établi que cette poussée est aussi puissante que le poids
du volume de liquide déplacé .
Un caillou est plus lourd qu'un volume égal d'eau donc il coule.
Un ballon est plus léger qu'un volume égal d'eau donc il flotte.
La loi d'Archimède permet même de savoir à quelle vitesse le caillou coule ou jusqu'où le ballon s'enfonce.
Combiné
à une étude des centres de gravité , son principe lui
permet d'expliquer des phénomènes très utiles en naviguation
.
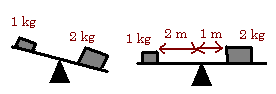
Les
lois du levier : il
pouvait , en appliquant sa théorie , construire des machines capables
de soulever des poids très lourds . Son étude se base sur le
principe de l'équilibre de deux objets posés de chaque côté
d'une balançoire : pour rester en équilibre , il faut mettre
l'objet le plus lourd plus près du milieu .Si par exemple , un objet
est deux fois plus lourd qu'un autre , il devra être placé deux
fois plus près du milieu . Archimède a donc construit une théorie
mathématique de l'équilibre de deux corps , basée sur
la notion de centre de gravité . Il est donc le précurseur
du barycentre de deux points.
Une telle théorie constitue aujourd'hui les bases de la partie de la mécanique appelée" la statique".
Qu'a-t-il
trouvé en tant qu'ingénieur ?
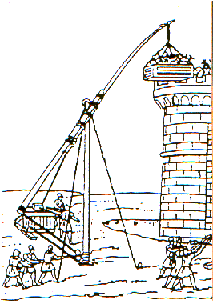
Les
machines de traction : il
releva un défi de manier seul une galère qui demande en général une douzaine
d’hommes.
Grâce
à un système ingénieux de poulies, leviers et palans, il réussit à prouver
qu’une petite force peut déplacer quelque chose de très gros, contrairement
à ce qu’avait affirmé Aristote.
Il
a créé la vis sans fin : la vis sans fin
permet de ramener à la surface de l'eau souterraine . Il aurait mis
au point cette invention lors d'un voyage en Egypte . Plusieurs historiens
de l'Antiquité racontent comment les habitants du bord du Nil arrosaient
leurs terrains grâce à cette vis , appelée aussi limaçon
, en raison de sa forme .
Le
planétaire
: grâce à
un système de roues dentées , il a construit une reproduction
miniature de l'Univers . En actionnant cette machine , les astres ( Soleil
, Lune ainsi que la plupart des planètes connues à l'époque
) se déplacent en reproduisant leurs mouvements réels dans le
ciel .
Les
machines de guerre
: il mit au point
une série de catapultes pendant le siège de Syracuse ( afin que les Syracusains
puissent défendre la ville contre les Romains ) sur le principe des
leviers.
et 
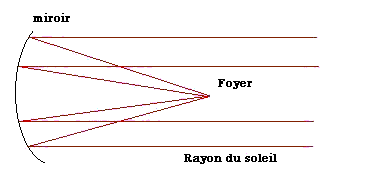
Il
mit au point des miroirs paraboliques
pour brûler les
vaisseaux ennemis qui attaquaient la ville .
Il écrivit des ouvrages :