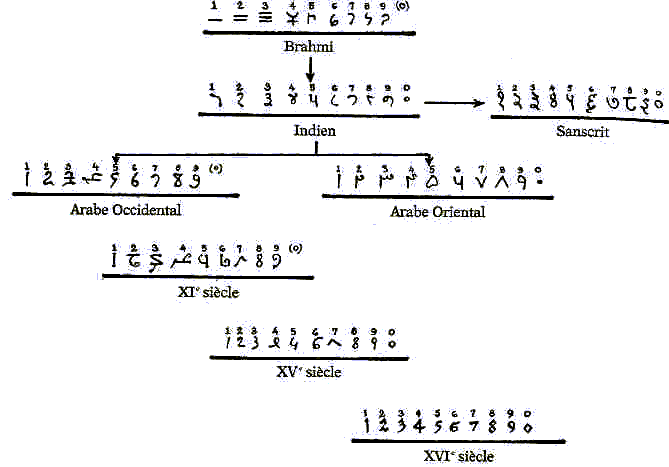
Au Ve siècle : naissance de notre système de numération moderne avec ses bases de calcul écrit tel que nous le pratiquons aujourd'hui .

Al - Khuwarizmi décrivit en détail le système indien dans " le livre des additions et des soustractions selon les méthodes indiennes " ; c'est le premier texte connu sur les chiffres indiens et le principe de position . Les arabes conservèrent la manière indienne d'écrire les chiffres ( de gauche à droite ) alors qu'ils écrivaient de droite à gauche .

Vers 972 , le moine français gerbert d'Aurillac , passionné de mathématiques , avait déjà fait une tentative pour introduire les chiffres français en Europe ; il n'eut pas de succès . Ce sera seulement à la fin du XIVe siècle que les négociants d'Angleterre et du Nord de l'Europe se décidèrent à l'adopter .

Dans la vieille numération indienne , c'était le principe d'addition qui était utilisé et non le principe de position .

Il existait un chiffre particulier pour chaque dizaine , chaque centaine , chaque millier et chaque dizaine de milliers .

Les dix chiffres étaient notés :

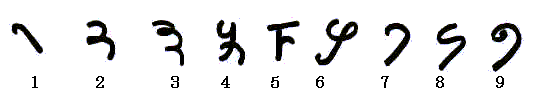
Par exemple , pour écrire 7629 :

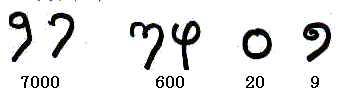
Pour 7.000 : le 1er symbole indique les milliers , le 2e symbole indique qu'il y en a sept. Pour 600 : le 1er symbole indique les centaines , le 2e symbole indique qu'il y en a six.

On pouvait ainsi écrire tous les nombres de 1 à 99.999 ; mais une telle écriture rendait toute opération impossible.

Ils ont pratiqué une numération orale en donnant à chaque chiffre et à chaque puissance de dix un nom en sanskrit ( langue savante indienne ) :

Eka     dvi     tri     catur     panca     sat     sapta     asta     nava

  1            2          3           4              5            6            7             8             9             

 

Dasa     sata     sahasra     ayuta     laksa      prayuta     koti      vyarbuda     padma

 10          100         1.000            10.000     100.000      1.000.000    10.000.000   100.000.000     1.000.000.000

 

Dans notre système de numération , le million et le milliard jouent le rôle de base auxiliaire.

 

exemple : 7463 : tri   sat  dasa  catur  sata  sapta  sahasra

                          3 +  610     + 4100    +       71000

 

On peut remarquer que l’ordre dans lequel ils écrivaient les chiffres sont inversés par rapport à notre numération : les unités se trouvaient en 1e et non en dernière position .  

 

C’était les prémices de la numération de position.

 

Au Ve siècle , pour abréger les écritures , ils suppriment tous les mots : dasa , sata ; ….

Et , par exemple , le nombre 7463 devient : tri   sat   catur   sapta ,

ce qui sous-entend  3 + 6  10 + 4 100 + 7  1000

Afin d’éviter des répétitions , les Indiens ont utilisés des synonymes pour exprimer un même chiffre . Nous n’entrerons pas dans le détail .

 

La numération indienne est donc devenue une numération orale de position , et ce sera la seule de l’Histoire.

 

 

Il résidera un problème : comment exprimer l’absence d’unités ? Comment dire le nombre 605 par exemple ? Afin de palier à un tel manque , ils créeront le mot « sunya » signifiant le « vide ».

Ainsi , le mot 605 se dira : panca   sunya   sat

Après les Babyloniens et sans doute en même temps que les Mayas , les Indiens venaient eux aussi d’inventer le zéro .

 

 

 

La forme graphique des 9 chiffres indiens a été mal précisée durant de nombreux siècles ; c’est la raison pour laquelle les astronomes indiens ont continué à écrire les nombres en toutes lettres.

 

Pour faire des calculs , les Indiens utilisaient une sorte d’abaque à colonnes tracées dans du sable fin .

Ils n’utilisaient ni jetons , ni cailloux , mais les chiffres de leurs vieilles notations numériques . L’usage du zéro n’était , dans ce cas , pas nécessaire , puisque la colonne pouvait rester vide .

 

Au début du VIe siècle , les colonnes de l’abaque disparaissent . les neuf chiffres reçoivent une valeur variable dépendant de leur position dans les représentations numériques . Le zéro est symbolisé par un point ou un rond . Le zéro indien est né . Les nombres sont écrits dans le même sens que notre numération .

 

Les règles d’opérations avec l’abaque étaient longues et compliquées . A cause de l’effaçage , il était impossible de déceler d’éventuelles erreurs . En supprimant les colonnes , ils perfectionnèrent les règles de l’abaque .  Il faudra attendre quelques siècles pour que les bases de calcul soient les mêmes que celles de notre calcul actuel .

 

A partir du VIe siècle , ils utilisaient un quadrillage pour multiplier deux nombres :

 

 

 
 

( " Zéro , la biographie d'une idée dangereuse " de Charles Seife )