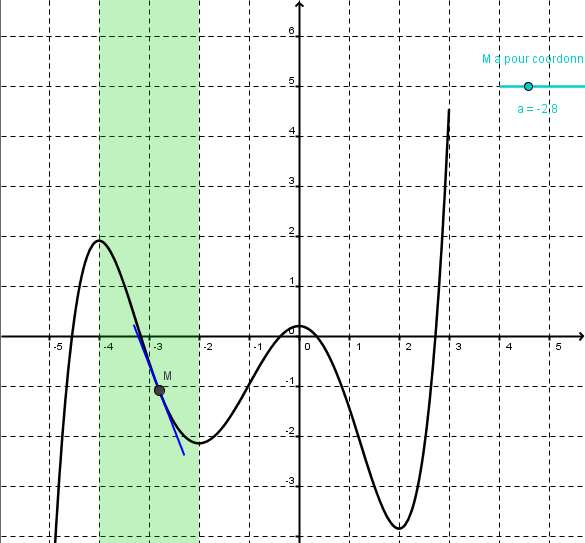
1. Lien entre la dérivation et le sens de variation
Percevoir que le nombre dérivé est lié au sens de variation de la fonction :
Visualiser cette animation qui rappelle cette notion : Consulter si vous y arrivez !
2. Un vidéo pour faire le point sur vos connaissances : https://www.blubbr.tv/game/index.php?game_id=64336&org=0#.VQFd7o6G_cw
3. Extremum d'une fonction : définition et détermination à l'aide de la dérivation. Regardez à partir de 33 min et 30 seconde durée 3 min environs.
Lien direct si la vidéo ci-dessus ne parche pas : http://www.youtube.com/watch?feature=player_detailpage&v=LNdHegdhT14#t=2016
4. Construction de vos savoirs :
- Lire le cours : PDF . Chercher à faire les démonstrations et bien comprendre les notions.
- Compléter le cours PDF (La correction est ici à voir après !!) Attention il y a un piège dans le document !! Allez vous le trouvez ?
- Compléter vos connaissances avec le livre pages 88 à 91.
- Construire votre propre cours et l'apprendre bien sur :)
Page à consulter : http://mathemitec.free.fr/animations/comprendre/derive/Derivee_fonction.php
5. Premier exemple : Etude d'une fonction du second degré (durée 4 min) :
6. Méthodologie : Déterminer le sens de variation d'une fonction polynome de degré 3 (durée 8 min).
7. Le cours complet mais un peu long !! (Durée 17 min)
8. Bilan de ce qu'il faut retenir (durée 5 min) :