
Accès rapide :
Introduction - La
numération - Evolution
du système de dénombrement - Les
jetons d argile - Les
gravures sur les tablettes d argile - Comment décoder les signes ? -
La numération en base
60 -
- les opérations
- en géométrie-
unités
de mesure
 Quand
ont-ils vécu ? d'environ 3.500 ans avant JC jusqu'au début
de notre ère , on retrouve des documents écrits aux alentours
de cette époque .
Quand
ont-ils vécu ? d'environ 3.500 ans avant JC jusqu'au début
de notre ère , on retrouve des documents écrits aux alentours
de cette époque .
 Où
? Babylone est située dans l'ancienne Mésopotamie ( actuel Irak )
bâtie il y a 2500 ans à 160 km de l'actuel Bagdad. Le Mésopotamie est la région
située entre les fleuves Euphrate et Tigre . Cette région est aujourd'hui
partagée entre deux pays , l'Irak et la Syrie. Entre 3.700 et 539 avant JC
, plusieurs civilisations se sont succédé en Mésopotamie : les Sumériens et
les Babyloniens entre autres.
Où
? Babylone est située dans l'ancienne Mésopotamie ( actuel Irak )
bâtie il y a 2500 ans à 160 km de l'actuel Bagdad. Le Mésopotamie est la région
située entre les fleuves Euphrate et Tigre . Cette région est aujourd'hui
partagée entre deux pays , l'Irak et la Syrie. Entre 3.700 et 539 avant JC
, plusieurs civilisations se sont succédé en Mésopotamie : les Sumériens et
les Babyloniens entre autres.
 Différents
peuples se sont succédés dans cette région : les
Sumériens et les Akkadiens , les Hittites , les Assyriens , les Chaldéens
, les Perses qui furent renversés par les armées d'Alexandre
le Grand. Les principales sources sur les mathématiques mésopotamiennes
datent de l'époques des Sumériens et des Akkadiens , on les
appelle mathématiques babyloniennes au vu de la place
clé de Babylone à cette époque .
Différents
peuples se sont succédés dans cette région : les
Sumériens et les Akkadiens , les Hittites , les Assyriens , les Chaldéens
, les Perses qui furent renversés par les armées d'Alexandre
le Grand. Les principales sources sur les mathématiques mésopotamiennes
datent de l'époques des Sumériens et des Akkadiens , on les
appelle mathématiques babyloniennes au vu de la place
clé de Babylone à cette époque .
 Le
nom "Mésopotamie" a été donné par l'historien grec Ploybe (
IIe siècle avant JC ) et signifie " le pays entre les fleuves "
( "mesos" : milieu et "potamos " : fleuve" )
Le
nom "Mésopotamie" a été donné par l'historien grec Ploybe (
IIe siècle avant JC ) et signifie " le pays entre les fleuves "
( "mesos" : milieu et "potamos " : fleuve" )
 Les
Sumériens sont les peuples de la Basse Mésopotamie . Les savoirs sumériens
et babyloniens sont connus grâce aux nombreuses tablettes d'argile gravées
en écriture cunéiforme ( en forme de " coins " ) relatant leur vie
sociale , religieuse , culturelle et scientifique .A cette époque ,
l'argile abondait en Mésopotamie et ces tablettes servaient de cahiers
d'exercices aux élèves. Tant que l'argile était humide
, les calculs pouvaient être effacés et refaits .Une fois sèches
, elles étaient abandonnées . Certaines étaient alors
réutilisées dans les fondations de bâtiments où
elles furent découvertes bien des siècles plus tard . Les mathématiques
babyloniennes sont nées des besoins concrets de la comptabilité
, de la finance et des poids et mesures.Plusieurs fouilles archéologiques
ont permis dès le 19e siècle de retrouver des centaines de tablettes
d'argile .
Les
Sumériens sont les peuples de la Basse Mésopotamie . Les savoirs sumériens
et babyloniens sont connus grâce aux nombreuses tablettes d'argile gravées
en écriture cunéiforme ( en forme de " coins " ) relatant leur vie
sociale , religieuse , culturelle et scientifique .A cette époque ,
l'argile abondait en Mésopotamie et ces tablettes servaient de cahiers
d'exercices aux élèves. Tant que l'argile était humide
, les calculs pouvaient être effacés et refaits .Une fois sèches
, elles étaient abandonnées . Certaines étaient alors
réutilisées dans les fondations de bâtiments où
elles furent découvertes bien des siècles plus tard . Les mathématiques
babyloniennes sont nées des besoins concrets de la comptabilité
, de la finance et des poids et mesures.Plusieurs fouilles archéologiques
ont permis dès le 19e siècle de retrouver des centaines de tablettes
d'argile .
L'argile de ces tablettes , tendre et
modelable , permettait des modifications et corrections , mais les inscritions
s'effaçaient par simple frottement .La conservation des quelques 320
tablettes retrouvées est dûe à des incendies qui ont cuit
l'argile . Celles-ci datent soit d'ente 1800 et 1500 avant JC , lors de la
première dynastie babylonienne , sous le règne d'Hammurabi ,
soit d'entre 600 avant JC et 300 après JC pendant les périodes
perse , hellénistique et romaine .
 L'écriture
serait née vers 3300 à Sumer et en Elam des nécessités
de l'administration et du commerce. La gestion des troupeaux , des grains
et des terres ; les ventes et les achats auraient peu à peu entraîné
une comptabilité , des contrats ... dont le nombre et la complexité
demandaient un enregistrement écrit. L'écriture est qualifiée
de "cunéiforme" ( en forme de coin ) . Au début le
sens de l'écriture était vertical de la droite vers la gauche
; puis vers 2600 il devint de gauche à droite et de haut en bas . Seule
l'écriture sur les monuments restera verticale.
L'écriture
serait née vers 3300 à Sumer et en Elam des nécessités
de l'administration et du commerce. La gestion des troupeaux , des grains
et des terres ; les ventes et les achats auraient peu à peu entraîné
une comptabilité , des contrats ... dont le nombre et la complexité
demandaient un enregistrement écrit. L'écriture est qualifiée
de "cunéiforme" ( en forme de coin ) . Au début le
sens de l'écriture était vertical de la droite vers la gauche
; puis vers 2600 il devint de gauche à droite et de haut en bas . Seule
l'écriture sur les monuments restera verticale.


La numération est née
du besoin d'écrire les nombres comme pour l'écriture .
 La
numération orale :
La
numération orale :
Elle est en base 60 . 60 et 1 sont désignés
par le même terme : gesh ou geshta .
| 1: guesh |
20: nish |
600 : gesh-ou ( 60  10 )
10 ) |
| 2: min |
30: oushou ( 3  10 )
10 ) |
1200 : gesh-ou-min ( 600  2 )
2 ) |
| 3: esh |
40 : nimin , nin ( 2  20 )
20 ) |
1800 : gesh-ou-esh ( 600  3 )
3 ) |
| 4: limmou |
50 : ninnou , nin-ou ( 40+10) |
............ |
| 5: ia |
60 : gesh , geshta |
3600: shar |
| 6: ash |
120 : gesh-min ( 60  2 )
2 ) |
7200: shar-min ( 3600  2 )
2 ) |
| 7: imin ( 5+2) |
180 : gesh-esh ( 60  3 )
3 ) |
........ |
| 8: issou |
...... |
36 000 : shar-ou (3600  10 )
10 ) |
| 9: illimou (5+4) |
|
........ |
| 10: ou |
|
216 000 : shar-gal |
Il subsiste des difficultés pour
construire les noms de certains nombres . Par exemple , pour 70 : "gesh-ou"
( 60 + 10 ) mais cela signifie 600 ( 60  10 ). Faut-il alors dire ou-gesh ?
10 ). Faut-il alors dire ou-gesh ?
 Les
comptables sumériens utilisaient des boulettes d'argile , appelées
"calculi" pour enregistrer les livraisons et les échanges
.Elles étaient enfermées dans des sachets d'argile clos et authentifiés
à l'aide d'un sceau .
Les
comptables sumériens utilisaient des boulettes d'argile , appelées
"calculi" pour enregistrer les livraisons et les échanges
.Elles étaient enfermées dans des sachets d'argile clos et authentifiés
à l'aide d'un sceau .

Plus
tard , le nombre de ces calculi est inscrit sur le sachet , puis sur des tablettes
d'argile .
Nous allons
voir comment faisaient les Sumériens pour dénombrer objets , bétail ....
 Apparition : un peu avant
le XVIIIe siècle avant JC
Apparition : un peu avant
le XVIIIe siècle avant JC
 numération
: additive
et de base
60 .
numération
: additive
et de base
60 .
De
1 à 59 , la numération est additive c'est-à-dire que les deux signes existant
( pour le 1 et le 10 ) sont répétés autant de fois que nécessaire . Au delà
de 59 , l'écriture devenait positionnelle : le signe du 1 eétait aussi
le signe du 60 , du 60  60 ...
60 ...
Ils ne connaissaient pas la virgule
et n'avaient aucune notation équivalente ; c'est le contexte qui indiquait
l'ordre de grandeur du nombre .
 Nécessité
d'un zéro ; il a existé plus tard.
Nécessité
d'un zéro ; il a existé plus tard.
 Les
tablettes babyloniennes sont de tailles variées : certaines font
5 cm de hauteur , d'autres 30 cm . Celles qui se sont le mieux conservées
sont celles qui ont été cuites dans des incendies . Il y en
a encore sans doute dans le Terre d'Irak .
Les
tablettes babyloniennes sont de tailles variées : certaines font
5 cm de hauteur , d'autres 30 cm . Celles qui se sont le mieux conservées
sont celles qui ont été cuites dans des incendies . Il y en
a encore sans doute dans le Terre d'Irak .
 Pour
les opérations , ils possédaient des tables d'inverses (
diviser par un nombre revient à multiplier par son inverse ) , mais
aussi des tables de carrés , de cubes , de sommes de carrés
et de cubes , des tables logarithmiques .
Pour
les opérations , ils possédaient des tables d'inverses (
diviser par un nombre revient à multiplier par son inverse ) , mais
aussi des tables de carrés , de cubes , de sommes de carrés
et de cubes , des tables logarithmiques .
 On
trouve essentiellement des résolutions de problèmes de la vie
de tous les jours , il n'y avait pas de concept abstrait . Les problèmes
sont :
On
trouve essentiellement des résolutions de problèmes de la vie
de tous les jours , il n'y avait pas de concept abstrait . Les problèmes
sont :
-
d'ordre financier:
calculs d'intérêts simples ou composés
-
d'ordre commercial
: bénéfices , échanges à valeurs égales
de produits
-
partage de domaines
entre héritiers
-
planification de
chantiers : fournitures , temps , transport , salaire ...
-
conversions d'unités
-
....
 Connaissances
des Babyloniens :
Connaissances
des Babyloniens :
Ils connaissaient des cas particuliers
de triplets pythagoriciens comme (3;4;5) ; (6;8;10) avec nos notations actuelles
en base 10 .Ils savaient seulement qu'ils pouvaient tracer des angles droits
avec de tels nombres , aucun besoin de le justifier , cela leur paraissait
naturel .
Ils connaissaient en géométrie
:
-
les surfaces du carré
, rectangles et triangle rectangle ;
-
les triangles équilatéraux
, hexagones , polygones réguliers et leur inscription dans un cercle
;
-
les volume du cube
, du pavé , du prisme , du cylindre , de la pyramide à base
carrée ...


Des
boules en argile creuses contenant des jetons d'argile de signification numérique
ont été retrouvées. Elles ont été remplacées plus tard par des tablettes gravées
, en argile . En effet , il fallait casser les boules pour en vérifier le
contenu , ce qui fut rapidement peu pratique .Ainsi , sont nés les plus vieux
chiffres connus de l'histoire. Des cercles et des encoches étaient utilisés
pour représenter des nombres. Quant à la nature du dénombrement , elle était
indiquée par un pictogramme.
Pour
graver sur les tablettes d'argile , ils utilisaient des calames de roseau.


impression
sur argile molle des signes de la numération sumérienne
Les
Sumériens utilisaient un mélange de base 10 et 60 pour représenter les nombres.
Il existait six jetons : ( ces "calculi" datent de 7.000 ans avant
JC )

On
remarquera que la bille à l'intérieur du grand cône ou de la sphère correspond
à une multiplication par 10.
exemple : pour représenter
le nombre 154 , décomposons 154 :
écrivons
la division euclidienne de 154 par 60 :
154
= 2  60
+ 34 = 2
60
+ 34 = 2  60 + 3
60 + 3  10 + 4
10 + 4
Ainsi
, le nombre 154 était représenté de la façon suivante :


Ces
jetons furent donc remplacés par les signes suivants sur les tablettes à partir
de la première moitié du 3e millénaire avant JC:



Vers
3100 avant JC , les tablettes d'argile étaient utilisées recto - verso :
¶
au recto : ils y inscrivaient les détails d'une opération
de comptabilisation
¶
au verso : ils y inscrivaient le total correspondant
, ainsi que le dessin correspondant au dénombrement effectué.
1°)
Comment trouver les significations des deux premiers signes ?
Après
de nombreuses vérifications et de multiples recoupements , ils ont pu déterminer
les signes correspondant à 1 et 10 .
2°)
Comment trouver le nombre 60 pour le 3e signe ?
Soit
x ce nombre cherché .
-
au recto , était gravé :

Ils
ont dénombré trois choses distinctes , soit en tout 10 + 5 + 30 + x + 40 =
x + 85
-
au verso , était gravé :
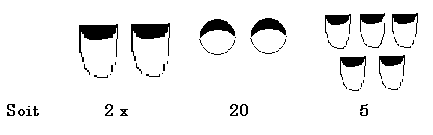
soit
en tout : 2x + 20 + 5 = 2 x + 25
Le
verso étant le récapitulatif du recto , on a donc : x + 85 = 2 x + 25
En
résolvant l'équation , on obtient bien : x = 60
Le principe
reste le même pour trouver les autres signes.
Ce sustème de numération
sera sans cesse amélioré et deviendra plus lisible avec la vulgarisation
, en Mésopotamie de l'écriture cunéiforme ,vers 2010
avant JC .
Il n'existait que deux
signes pour représenter tous ces nombres ( nous avons , pour comparaison
, les 10 chiffres pour écrire les nombres ) :
Ecrire 12 140 en base 60 , c'est comme convertir 12 140 secondes
en heures , minutes et secondes .
( 12140 s =... h... min.. s avec chacun des trois nombres strictement
inférieur à 60. Sur l'exemple ,
12 140 s = 3 h 22 min 20 s ) .On écrira donc 12140 en base
60 de la façon suivante : [ 3 ; 22 ; 20 ],
sous-entendu : 3  3600 + 22
3600 + 22  60 + 20
60 + 20
Ecriture en numération babylonienne
:
De 1 à 9 , les chiffres sont
obtenus par itération du symbole 1 .
De 10 à 59 , on répète
les symboles 1 et 10 autant de fois que nécessaire , par addition .C'est
la raison pour laquelle on l'appelle numération
de position .
60 s'écrit à l'aide d'un
symbole particulier : le même symbole que pour le 1 , d'où des
confusions de lecture.
A partir de 61 , c'est la numération
de position qui est appliquée , comme pour notre système de
numération : la 1e colonne correspond aux unités , la 2e aux
soixantaines , la 3e au rang des 60 60
, la 4e au rang des 60
60
, la 4e au rang des 60 60
60 60
... Les savants utilisaient des signes de séparation entre les colonnes
pour éviter les confusions .
60
... Les savants utilisaient des signes de séparation entre les colonnes
pour éviter les confusions .
Ce
système a engendré beaucoup d'erreurs : les nombres 63- 4 - 3603 - 3662 étaient
représentés par les même symboles dans le même ordre . Seul le contexte permettait
de comprendre le nombre .
.
Le
symbole désignant le vide n'existait pas encore , on signalait donc
par un espace l'absence d'unités d'un certain ordre , d'où la
confusion entre toutes ces écritures .
Ce
ne sera que vers IV siècle que sera inventé le
zéro le plus vieux de l'histoire de l'humanité .

-
Les additions
et les soustractions se faisaient sans difficultés .
-
Pour les multiplications
, ils possédaient des tables , établies par comptage ou par
tâtonnements .
-
Pour les divisions
, ils utilisaient des tables d'inverses.( diviser par un nombre revient
à multiplier par son inverse) .
Prenons un exemple : soit à effectuer
la division 165  15 , c'est-à-dire : 165
15 , c'est-à-dire : 165 
 .
.
On écrit 165 en base 60 : 165 =
2  60 + 45
60 + 45
donc 165  15 = 165
15 = 165 
 = 165
= 165 
 = ( 2
= ( 2  60 + 45 )
60 + 45 ) 
 =
( 2
=
( 2  60 )
60 ) 
 + 45
+ 45 
 =
8
=
8  1 + 3 = 11
1 + 3 = 11

Tablette mathématique
babylonienne montrant une table de multiplication
- Ils savaient résoudre des équations
du premier et du deuxième degré à une inconnue ainsi
qu'un système d'équations du premier degré à deux
inconnues , et ceci dans le cadre de problèmes de répartitions
de grains ou de calculs d'intérêts.( pour résoudre une
équation du second degré , ils utilisaient ce qui correspond
à notre méthode actuelle de "complétion du carré
" , se fondant sur le fait qu'on peut toujours découper un rectangle
pour former un carré ) .
- 3 était considéré comme une valeur
approchée de pi .

-
Depuis le deuxième
millénaire , ils savaient calculer des surfaces de carrés
( en fonction du côté ) , de rectangles ( en fonction de la
longueur et de la largeur ) et de trapèze ( numériquement
) .
-
Ils connaissaient
une formule approchée pour calculer le volume du tronc d'une pyramide
à base carrée .
-
Ils savaient , sans
autre chose , qu'un triangle de côtés 3 , 4 et 5 est un triangle
rectangle .
-
Ils savaient calculer
la diagonale du carré , et connaissaient une formule approchée
pour calculer celle du rectangle .
-
Ils savaient appliquer
numériquement le théorème de Thalès ( non connu
à l'époque bien entendu )

![]() Quand
ont-ils vécu ? d'environ 3.500 ans avant JC jusqu'au début
de notre ère , on retrouve des documents écrits aux alentours
de cette époque .
Quand
ont-ils vécu ? d'environ 3.500 ans avant JC jusqu'au début
de notre ère , on retrouve des documents écrits aux alentours
de cette époque . ![]() Où
? Babylone est située dans l'ancienne Mésopotamie ( actuel Irak )
bâtie il y a 2500 ans à 160 km de l'actuel Bagdad. Le Mésopotamie est la région
située entre les fleuves Euphrate et Tigre . Cette région est aujourd'hui
partagée entre deux pays , l'Irak et la Syrie. Entre 3.700 et 539 avant JC
, plusieurs civilisations se sont succédé en Mésopotamie : les Sumériens et
les Babyloniens entre autres.
Où
? Babylone est située dans l'ancienne Mésopotamie ( actuel Irak )
bâtie il y a 2500 ans à 160 km de l'actuel Bagdad. Le Mésopotamie est la région
située entre les fleuves Euphrate et Tigre . Cette région est aujourd'hui
partagée entre deux pays , l'Irak et la Syrie. Entre 3.700 et 539 avant JC
, plusieurs civilisations se sont succédé en Mésopotamie : les Sumériens et
les Babyloniens entre autres. ![]() Différents
peuples se sont succédés dans cette région : les
Sumériens et les Akkadiens , les Hittites , les Assyriens , les Chaldéens
, les Perses qui furent renversés par les armées d'Alexandre
le Grand. Les principales sources sur les mathématiques mésopotamiennes
datent de l'époques des Sumériens et des Akkadiens , on les
appelle mathématiques babyloniennes au vu de la place
clé de Babylone à cette époque .
Différents
peuples se sont succédés dans cette région : les
Sumériens et les Akkadiens , les Hittites , les Assyriens , les Chaldéens
, les Perses qui furent renversés par les armées d'Alexandre
le Grand. Les principales sources sur les mathématiques mésopotamiennes
datent de l'époques des Sumériens et des Akkadiens , on les
appelle mathématiques babyloniennes au vu de la place
clé de Babylone à cette époque . ![]() Le
nom "Mésopotamie" a été donné par l'historien grec Ploybe (
IIe siècle avant JC ) et signifie " le pays entre les fleuves "
( "mesos" : milieu et "potamos " : fleuve" )
Le
nom "Mésopotamie" a été donné par l'historien grec Ploybe (
IIe siècle avant JC ) et signifie " le pays entre les fleuves "
( "mesos" : milieu et "potamos " : fleuve" ) ![]() Les
Sumériens sont les peuples de la Basse Mésopotamie . Les savoirs sumériens
et babyloniens sont connus grâce aux nombreuses tablettes d'argile gravées
en écriture cunéiforme ( en forme de " coins " ) relatant leur vie
sociale , religieuse , culturelle et scientifique .A cette époque ,
l'argile abondait en Mésopotamie et ces tablettes servaient de cahiers
d'exercices aux élèves. Tant que l'argile était humide
, les calculs pouvaient être effacés et refaits .Une fois sèches
, elles étaient abandonnées . Certaines étaient alors
réutilisées dans les fondations de bâtiments où
elles furent découvertes bien des siècles plus tard . Les mathématiques
babyloniennes sont nées des besoins concrets de la comptabilité
, de la finance et des poids et mesures.Plusieurs fouilles archéologiques
ont permis dès le 19e siècle de retrouver des centaines de tablettes
d'argile .
Les
Sumériens sont les peuples de la Basse Mésopotamie . Les savoirs sumériens
et babyloniens sont connus grâce aux nombreuses tablettes d'argile gravées
en écriture cunéiforme ( en forme de " coins " ) relatant leur vie
sociale , religieuse , culturelle et scientifique .A cette époque ,
l'argile abondait en Mésopotamie et ces tablettes servaient de cahiers
d'exercices aux élèves. Tant que l'argile était humide
, les calculs pouvaient être effacés et refaits .Une fois sèches
, elles étaient abandonnées . Certaines étaient alors
réutilisées dans les fondations de bâtiments où
elles furent découvertes bien des siècles plus tard . Les mathématiques
babyloniennes sont nées des besoins concrets de la comptabilité
, de la finance et des poids et mesures.Plusieurs fouilles archéologiques
ont permis dès le 19e siècle de retrouver des centaines de tablettes
d'argile .![]() L'écriture
serait née vers 3300 à Sumer et en Elam des nécessités
de l'administration et du commerce. La gestion des troupeaux , des grains
et des terres ; les ventes et les achats auraient peu à peu entraîné
une comptabilité , des contrats ... dont le nombre et la complexité
demandaient un enregistrement écrit. L'écriture est qualifiée
de "cunéiforme" ( en forme de coin ) . Au début le
sens de l'écriture était vertical de la droite vers la gauche
; puis vers 2600 il devint de gauche à droite et de haut en bas . Seule
l'écriture sur les monuments restera verticale.
L'écriture
serait née vers 3300 à Sumer et en Elam des nécessités
de l'administration et du commerce. La gestion des troupeaux , des grains
et des terres ; les ventes et les achats auraient peu à peu entraîné
une comptabilité , des contrats ... dont le nombre et la complexité
demandaient un enregistrement écrit. L'écriture est qualifiée
de "cunéiforme" ( en forme de coin ) . Au début le
sens de l'écriture était vertical de la droite vers la gauche
; puis vers 2600 il devint de gauche à droite et de haut en bas . Seule
l'écriture sur les monuments restera verticale.![]() La
numération orale :
La
numération orale : 










