Riemann

Accès rapide :

Qui était Riemann ?

Bernhard RIEMANN est né en 1826 dans un village du royaume de Hanovre. Il fit ses études et une courte carrière universitaire à Göttingen avant de passer en Italie pour soigner sa maladie pulmonaire. En 1866, il fut enterré près du Lac Majeur

A sa mort, son oeuvre fut publiée en un seul volume car ses travaux souvent intuitifs sont incomplets. Les démonstrations sont dans la plupart des cas absentes. Pourtant la nouveauté des notions et des méthodes donnèrent aux mathématiques un élan novateur qui changa profondément les conceptions des mathématiques.

Il s'intéressa comme la plupart des mathématiciens de son époque, à la physique, et publia des ouvrages sur la loi de répartition de l’électricité statique, l’électrodynamique, la propagation des ondes atmosphériques planes, la mécanique de l’oreille entre autres.

Que lui doit-on ?

L'intégrale de Riemann :

Il s'agit au départ d'une approche géometrique en calculant l'aire sous la courbe d'une fonction f définie sur un segment [a;b].

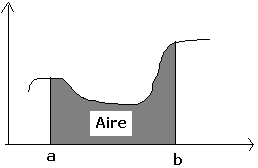
Il reprend l'idée de Cauchy en remplaçant l'aire cherchée par la somme des aires de rectangles judicieusement choisies.

Il découpe [a;b] en une suite de sous-intervalles ayant une extrémité en commun. Ensuite sur chacune de ces bases, il construit un rectangle de hauteur f(z) avec z un point quelconque de la base ( en particulier le milieu)

On obtient donc une approximation de l'aire sous la courbe en additionnant les surfaces des rectangles ; plus les bases sont petites plus cette approximation est précise.

Par définition, quand la longueur de la plus grande des bases tend vers zéro, cette somme des aires de rectangle est égale à l'intégrale de Riemann sur [a;b] et est noté depuis Leibniz .

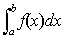Il fit considérablement évoluer les mathématiques par ses travaux dans de nombreux domaines : fonctions analytiques, intégrales d’Abel, topologie et géométrie différentielles, etc. Sa géométrie sphérique est à l’origine de la géométrie non euclidienne : deux perpendiculaires à une droite se coupent, de sorte que toute droite est finie. Cette géométrie est adéquate pour rendre compte de la structure de l’univers.