Nombre d’or et triangle isocèle
Nombre d’or et pentagone régulier
Nombre d’or et décagone régulier
Le nombre d’or est
égal à 
,
on le note 
;
il est l'une des deux solutions
de l’équation x² - x - 1 = 0 ; la deuxième
solution de l'équation étant égale à 
,
c'est-à-dire à - 1 /
.
Le nombre d'or a une propriété bien particulière :Chaque puissance est la somme des deux précédentes :
²
=
+ 1 ; 
=
2
+ 1 ; 
=
3
+ 1 ; 
=
5
+ 3 ....
Quand est apparu pour la première fois ce nombre d’or ?
Au IIIe siècle avant JC , Euclide écrivait dans « Eléments » : « Couper une droite donnée de telle sorte que le rectangle contenu par la droite soit égal au carré sur le segment restant ». Mais il ne nomme pas ce rapport .
Euclide partage
une portion de droite AC en " extrême et moyenne raison "
: il cherche le point B tel que 
L'une des deux solutions
de cette équation est bien x =
La lettre grecque
est
l’initiale de Phidias , sculpteur grec , qui décora
au Ve siècle avant JC le
Parthénon d’Athènes .
Qu’est-ce que le rectangle d’or ?
Un
rectangle est appelé rectangle d’or si le rapport entre sa longueur et sa
largeur est égal au nombre d’or .
ABCD est un
carré de côté l ;
On trace un
arc de cercle de centre E et de rayon CE ; il coupe (AB) en F.
On construit
alors G tel que ADGF soit un rectangle.
ADGF est un rectangle d’or .
Démonstration :
Montrons que
.
AB = l donc EB =
.
En utilisant le théorème de Pythagore dans le triangle ECB rectangle en B , on calcule EC :
EC =
l donc EF = l
Finalement
, 
.
ADGF est donc
bien un rectangle d’or
Comment
construire le nombre d’or ?
Il suffit d’appliquer
la construction du rectangle d’or avec AB = 1 .Le segment [AF] a alors pour
longueur le nombre d’or .
Le
nombre d’or dans la nature
& La pyramide de Khéops : le rapport de sa hauteur
par sa demi-base est égal au nombre d’or
( la base de la pyramide est un carré )
& Le Parthénon , construit au Ve siècle avant
JC : il s’inscrit dans un rectangle d’or .
& Chez les plantes : les fleurs de tournesol de
même taille présentent 89 spirales dans un sens et 144 dans l’autre et 144
89 
1,617977
Nombre
d’or et triangle isocèle
ABC est un triangle isocèle en A tel que les deux angles B et C soient égaux à 36 °.
On a BC ¸ AC
=
Démonstration :
On trace la
droite (AI) avec I milieu de [BC] et
(AI) ^ (BC) .
Cos B = 
donc
cos 36 ° = .
Or
, cos 36° =
D’où : 
=
.
Donc 
On a donc bien
BC ¸ AB = pour ABC isocèle en A avec
les angles à la base égaux à 36°.
Un tel triangle
est appelé triangle d’or .
Nombre
d’or et pentagone régulier
Un pentagone
régulier est un polygone avec 5 côtés égaux
.
Le rapport
entre une diagonale du pentagone et un côté est égal au nombre d’or .
Les cinq angles
sont égaux à 108 ° .
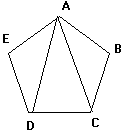
Démonstration :
Il suffit d’utiliser
le triangle AED isocèle en E .
L’angle E =
108°
Les deux angles
à la base A et D sont donc égaux à :
(180 - 108)
2
=36°
En utilisant
ce qui précède sur le triangle d’or , on obtient directement : 
Nombre
d’or et décagone régulier
Un décagone
régulier est un polygone avec 10 côtés égaux
.
Le rapport
entre le rayon du cercle circonscrit
au décagone régulier et l’un de ses côtés est égal au nombre d’or ;
c’est-à-dire OA AB
=
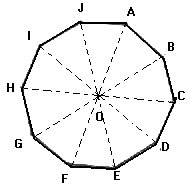
Le décagone est formé de 10 triangles
isocèles identiques et l’angle O du sommet principal est égal à 360 10 = 36°.
Les deux angles
à la base de chacun de ces triangles isocèles sont égaux à : ( 180 -
36 ) 2
= 72°
Or cos 72 ° = 2 cos ² 36° - 1 = 2 ( )
² - 1 = … = 
(
cos 2a = 2 cos ² a - 1 )
Donc AI / AC
= donc
AC / AI = 
Donc AC / AB
= AC / 2 AI =
est
une première façon d'approcher le nombre d'or.
.