Exercice 1: calcul des décimales de pi  

 

Partie I  

Ptolémée , mathématicien grec du Ie siècle après JC , a calculé la longueur d’une corde de cercle de rayon donné et d’angle au centre donné. Voyons cette méthode :

 

On considère un polygone régulier à n côtés inscrit dans un cercle de rayon r .

Soit H pied de la hauteur issue de O dans le triangle ( Pour des raisons de commodités , c’est un hexagone qui est représenté ici ) .  

1°) Donner la mesure de l’angle en fonction de n .

2°) Donner la mesure de l’angle en fonction de n .

3°) a) En utilisant le sinus de l’angle , exprimer HB en fonction de n et de r .

     b) En déduire AB en fonction de n et de r .

4°) a) Montrer que le périmètre de ce polygone s’écrit : P = 2 n r sin (180n) 

      b) Exprimer en fonction de r le périmètre du cercle .

5°) Comparer le périmètre du polygone et du cercle de rayon 1 pour :

a)     10 côtés .

b)     30 côtés .

6°) Que peut-on dire sur les périmètres du polygone et du cercle si on considère un polygone avec un  grand nombre de côtés ?

Partie II

 

C’est Archimède , mathématicien grec , qui a trouvé une méthode pour calculer les décimales de .

Sa méthode consiste à encadrer un cercle de diamètre 1 ( dans ce cas , le périmètre est égal à  )par deux polygones réguliers inscrits et circonscrits à ce cercle . Archimède a considéré successivement des polygones  à 6 ; 12 ; 24 ; 48 et 96 côtés ( le nombre de côtés est doublé à chaque fois ). Ainsi , vers 250 avant JC , il montre que  est compris entre 223/71 et 22/7. 

Grâce à sa méthode , on a pu déterminer les décimales de  ( plus de 50 milliards de décimales de  en 1997).

Nous utilisons ici la trigonométrie ; Archimède a utilisé une méthode purement géométrique .

On considère un polygone régulier à n côtés inscrit dans un cercle de rayon 1 .

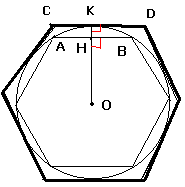
Soit n le nombre de côtés du polygone ( n étant égal à 6 ; 12 ; 24 ; 48 ou 96 côtés pour Archimède )

 

La première partie a permis de calculer le périmètre du polygone régulier inscrit dans le cercle . Dans cette deuxième partie , on va calculer le périmètre du polygone circonscrit au cercle .

1°) Si le diamètre du cercle est égal à 1 , montrer que le périmètre du polygone régulier inscrit dans le cercle est égal à P = n sin (180n) 

                                                                             

2°) Donner la mesure de l’angle en fonction de n .

3°) Donner la mesure de l’angle en fonction de n .

4°) a) En utilisant la tangente de l’angle , exprimer KD en fonction de n .

     b) En déduire CD en fonction de n .

5°) Montrer que le périmètre de ce polygone s’écrit : P = n tan (180n) 

6°) En déduire un encadrement de en utilisant les questions 1 et 5 .

7°) Donner un encadrement de pour n = 96 ( valeur de trouvée par Archimlède ) ; puis pour n = 1536

 

 

Exercice 2 : calcul des sinus , cosinus et tangente à la manière d'Hipparque  

 

1°) ABC est un triangle équilatéral de côté . Soit H le pied de la hauteur issue de A . 

a)     Exprimer en fonction de , le cosinus de l’angle .

b)     En déduire que cos 60° = 0,5

c)      En déduire les valeurs exactes de sin 60° et tan 60 ° . 

 

2°) Hipparque a démontré que (cos a ) ² = ( 1 + cos 2a )  2

a)     Utiliser cette formule pour calculer les valeurs exactes de : cos 30° ; cos 15 ° .

     ( Vous écrirez cos 30° sous la forme )

b)     Calculer alors les valeurs exactes de sin 30° ; sin 15° ; tan 30° ; tan 15 ° .

 

3°) Hipparque a aussi montré que cos (a+b ) = cos a  cos b – sin a sin b

a)     Utiliser cette formule pour calculer cos 45° .

b)     Calculer alors sin 45° et tan 45° .

 

4°) ABC est un triangle rectangle en A . Soit x la mesure de l’angle .

a)     En écrivant les définitions de cos et sin , montrer que sin (90 – x) = cos x

b)     En écrivant les définitions de sin et cos , montrer que cos (90 – x) = sin x

c)      Déduire des deux questions précédentes que tan (90 – x ) =

5°) En utilisant les résultats de la question précédente ainsi que ceux de la question 2 , calculer les valeurs exactes de : cos 75° , sin 75 ° et tan 75 °.

 

Remarque : C’est avec ces formules , entre autres , qu’Hipparque a calculé les valeurs des sinus , cosinus et tangentes des angles que nous donnent aujourd’hui les calculatrices .