Exercice
1 : construction d'une racine carrée à la règle
1°) On veut construire à la règle et à l’équerre et de façon exacte un segment
de longueur
cm.
En remarquant que 13 = 3² + 2² , et en
justifiant votre construction , construire
un tel segment.
2°) En s’inspirant de la question 1 , sans justifier, mais en indiquant les longueurs choisies sur le dessin, construire à la règle et à l’équerre et de façon exacte un segment de longueur :
a) cm
b) 
cm c) 
cm d) 
cm
3°) a) On veut construire à la règle et
à l’équerre et de façon exacte un segment de longueur 
cm.
En s’inspirant de la question 1 , mais en utilisant cette fois une soustraction , et en justifiant votre construction , construire un tel segment.
b) De même , construire un segment de longueur
cm ;
puis 
cm
.
Exercice
2 : La spirale d'Archimède
1°)
Calculer les longueurs AB ; BC ; CD et DE .
2°)
Continuer le procédé pour construire
un segment de longueur 
cm.
3°)
De façon générale , on veut construire la racine carrée d’un nombre impair
n .
a)
Démontrer que n = 
b)
Utiliser le résultat du a) et s'inspirer des questions précédentes
pour construire à la règle et au compas : et 
Exercice
3 : anciennes unités de mesure et nombre d'or
Au
Moyen-Age , les bâtisseurs de cathédrales utilisaient un instrument de mesure
de longueurs ressemblant à une règle articulée
avec pour unités : la paume , la palme , l’empan , le pied et
la coudée .
Une
des anciennes unités de longueur est la ligne équivalent à 0,2247 cm.
La
paume = 34 lignes ( largeur de la paume de la main )
La
palme = 55 lignes ( distance maximale
entre l’index et l’annulaire )
L’empan
= 89 lignes ( distance maximale entre
le pouce et l’auriculaire )
Le
pied = 144 lignes
La
coudée = 233 lignes ( distance du coude au bout des mains )
2°)
Comparer avec le nombre d’or 
.
Exercice
4 : Les lunules d'Hippocrate
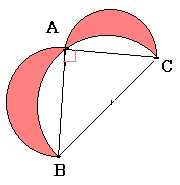
On donne BC = a cm AC = b cm et
AB = c cm
Exprimer en
fonction de a , b et c :
1°) l’aire
A du triangle ABC ;
2°) l’aire
A1 du demi-disque de diamètre [AB] ;
3°) l’aire
A2 du demi-disque de diamètre [AC] ;
4°) l’aire
A3 du demi-disque de diamètre [CB] .
5°) En déduire
que A1 + A2 = A3
6°)En déduire
que l’aire de la partie hachurée appelée lunules 
est
égale à l’aire du triangle .
Exercice
5: Le nombre d'or
Le nombre d’or
, noté 
(« phi »)
, est égal à .
1°) a) Donner un arrondi de au
millième .
b) Démontrer que ²
= +
1
c) Démontrer que 1 / = -
1
2°) On veut construire à la règle et au compas , et de façon exacte , un segment de longueur égal au nombre d’or .
a)
Effectuer la construction
suivante :
-
tracer un rectangle
ABCD de centre O tel que AB = 2 cm et BC = 1 cm
-
Soit I le pied
de la hauteur issue de O dans le triangle DOC .
-
Tracer le cercle
de centre O et tangent à [CD] .
-
Le cercle coupe
le segment [AC] en R et S , R étant
le point le plus proche de A .
On va montrer dans les questions suivante que CR = .
Repasser ce segment en couleur et vérifier
qu’il est bien égal à 1,6 cm environ ( qui est la valeur approchée au dixième
du nombre d’or )
b)
Calculer AC ;
en déduire OC .
c)
Calculer OI ;
en déduire OR .
d)
En déduire la
valeur exacte de CR exprimée sous la forme d'une fraction .
Exercice
6 : Le rectangle d'or
Un
rectangle est appelé rectangle d’or si le rapport entre sa longueur et sa
largeur est égal à .
1°)
Construction d’un rectangle d’or
a) Soit
ABCD un carré et I milieu de [DC].
Le cercle de centre I et de rayon
IB coupe la demi-droite [DC) en E .
Faire une figure.
b) Construire
le point F tel que ADEF soit un rectangle .
On va vérifier dans la question suivante
que ADEF est un rectangle d’or .
2°)
Justification de la construction
On appelle L la longueur de ce rectangle
et l sa largeur .
a)
Exprimer IB en fonction de l .
b)
En déduire L en fonction de
l .
Vérifier
qu’on a bien 
=
1°)
Soit ABC un triangle rectangle en A . Soit H pied de la hauteur issue de A
.
On va démontrer que : AH² = BH 
CH
a)
Ecrire le théorème
de Pythagore dans le triangle ABC .
b)
Ecrire le théorème de Pythagore dans le triangle
ABH .
c)
Ecrire le théorème
de Pythagore dans le triangle AHC .
d)
En déduire que
BC² = 2 AH² + HB² + HC²
e)
En écrivant que
BC = BH + HC , montrer que BC² = BH² + HC² + 2 HB HC
f)
Déduire des questions
d) et e) que : AH² = BH CH
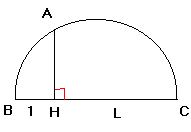
2°)
On veut construire à la règle et au compas un segment de longueur : 
cm
a)
Construire un
segment [BC] de longueur (1 + L) cm et H un point de [BC] tel que BH = 1 cm
b)
Construire un
demi-cercle de diamètre [BC]
c)
Construire la
droite perpendiculaire à (BC) passant par H . Elle coupe le demi-cercle en
A .
d)
En utilisant la
question 1°) , montrer que : AH = cm
3°)
En appliquant le même type de construction qu’au 2°) , construire un segment
de longueur exactement égal à :
a) 
cm b) 
cm