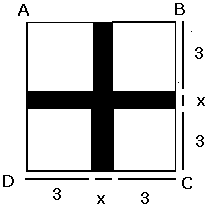
Exercice 1: résolution d'une équation avec une méthode arabe du IXe siècle

 

On se propose de résoudre l’équation  x² + 12 x = 64

 

« Sur chaque côté d’un carré de côté , tracer 4 rectangles de dimensions et 3 ( 3 étant le quart de 12 , 12 étant le coefficient de dans l ‘équation que l’on cherche à résoudre). »

 

1°)  Démontrer que l’aire de la partie coloriée est égale à x² + 12 x                                             

2°)  a) Exprimer de deux façons différentes l’aire du carré ABCD .                                              

       b) En déduire que résoudre l’équation x²+12x=64 revient à résoudre (x+6)²=100             

       c) En déduire la valeur de .                                                                                                     

3°) Appliquer la même méthode pour résoudre l’équation:x²+16x =17                                                                                                                        

4°) Peut-on résoudre de même l’équation x² -4 x = 12? Quelle est alors la limite de cette méthode ?    

 

---