Vers
200 avant JC , Eratosthène , mathématicien grec , a calculé
le périmètre de la Terre :
- Un jour dans l’année , il remarque que le Soleil éclaire le
fond d'un puits à Syène ( En Egypte , actuellement Assouan)
, c’est-à-dire que les rayons sont verticaux .
- Ce même jour , à Alexandrie , à 785 km environ de Syène
, une tour de 25 m de haut fait une ombre de 3,1 m .
Pour calculer la circonférence de la Terre , il a lui fallait connaître
l’angle
, puis connaissant la longueur de l’arc 
,
il en a déduit la circonférence de la Terre .
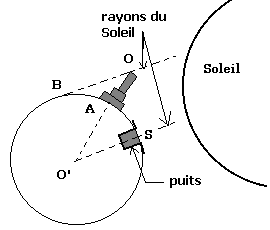
A : Alexandrie , S : Syène, O’ : centre de la Terre , OA
: hauteur de la tour , AB : ombre de la tour
1°) On suppose que l’arc 
est un segment et que OAB est un triangle rectangle en A .
Démontrer que l’angle 
.
est égal à 7,2° environ ( valeur trouvée par Eratosthène
)
2°) Pourquoi les angles et
sont-ils
égaux ?
3°) a) En déduire une valeur approchée de la circonférence
de la Terre en km .
b) En déduire une valeur approchée au millième du rayon
de la Terre .
4°) Il faut savoir qu’à l’époque où Eratosthène
a calculé la circonférence de la Terre , le mètre n ‘existait
pas . C’était le stade qui était utilisé comme unité
de longueur.
Sachant qu’un stade 
157
m , quelle est la longueur en stades de la circonférence de la Terre
trouvée par Eratosthène ?
5°) Vérifier le résultat trouvé en regardant dans
une encyclopédie le rayon de la Terre actuellement calculé par
les scientifiques.