Triangles semblables et isométriques
I Bilan de la géométrie dans le plan.
1) Les triangles.
Somme des angles d’un triangle.
Médianes et centre de gravité G
Bissectrices et cercle inscrit. I
Médiatrices et cercle circonscrit O
Hauteurs et orthocentre H
Propriétés des triangles isocèles et équilatéraux.
Ex 7/
2) Théorème de pythagore.
Le théorème permet de calculer la longueur d’un troisième coté dans le triangle rectangle, sa réciproque permet de démontrer qu’un triangle est rectangle et sa contra posé de démontrer qu’un triangle n’est pas rectangle !
En fonction du résultat à atteindre, on ne rédige pas de la même façon.
Ex 4/
3) Théorème de thalès.
A savoir le théorème des milieux.
Le théorème de thalès permet de calculer une distance alors que sa réciproque permet de démontrer que deux droites sont parallèles et sa contra posé que deux droites ne sont pas parallèles !
Ex 5/8/9
4) Trigonométrie.
Les formules permettent de calculer soit des angles soit des longueurs dans des triangles rectangles.
Il faut connaître SOHCAHTOA ; cos² +sin ² = 1 tan = sin/cos ainsi que le tableau de valeur :
|
X en degré |
30° |
45° |
60° |
|
Cos x |
Sqr3 /2 |
Sqr2 /2 |
½ |
|
Sin x |
½ |
Sqr2 /2 |
Sqr3 /2 |
|
Tan x |
Sqr3 /3 |
1 |
Sqr 3 |
5) Les angles.
Angles alternes-internes ; correspondants ; opposés par le sommet
Angles inscrits : AMB est dit inscrit dans le cercle C si le triangle AMB est inscrit dans le cercle C.
Dessin :
On dit que AOB est l’angle au centre associé à l’angle AMB. [AB] est une corde AB un arc.
A savoir : AMB = ½ AOB et AMB = ANB soit :
Dans un cercle , un angle inscrit est égal à la moitié de l’angle au centre associé.
Dans un cercle , deux angles inscrits qui interceptent le même arc sont égaux.
Ex 6
II triangles isométriques.
Activité du livre p.
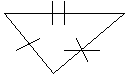
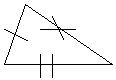
1. Définition : On dit que deux triangles sont isométriques s’ils ont leurs côtés respectifs de même longueur.
 |
|||
 |
|||
Vocabulaire : On dit que les côtés [AB] et [A’B’] sont homologues.
Ils existent deux autres paires de côtés homologues…
On dit aussi que les angles A et A’ sont homologues.
2. Propriétés
P1 : Si deux triangles sont isométriques alors leurs angles homologues sont égaux deux à deux.
Rem : la réciproque de cette propriété est fausse.
Exemple :
Propriété 2: Deux triangles isométriques ont la même aire.
P3 : Pour que deux triangles soient isométriques, il suffit que l’un des deux soit l’image de l’autre par une translation, une rotation ou une symétrie ( axiale ou centrale)
Vocabulaire : On appelle isométrie les transformations qui conservent les longueurs ;
Ex translation,…
Ces trois transformations étant des isométries, l’images d’un segment est un segment de même longueur…
3.Déterminations de triangles isométriques.
Rappel de cinquième sur les conditions nécessaire et suffisantes pour construire un unique triangles.
Th1 : Si deux triangles ont un côté égal compris entre deux angles respectivement égaux, alors ils sont isométriques.
Th2. : Si deux triangles ont un angles égal compris entre deux côtés respectivement égaux, alors ils sont isométriques.
III Triangles semblables.
1) Définition :
On dit que deux triangles sont semblables si ils ont des angles égaux deux à deux.
Rem : Si deux triangles sont isométriques alors ils sont semblables amis la réciproque est fausse.
2) Propositions :
Th1 : Si deux triangles ont 2 angles égaux deux à deux alors ils sont semblables
Démo : A faire par les élèves .
Th 2 : Si deux triangles sont semblables alors les côtés opposés aux angles égaux sont proportionnels.
Admis.
Th 3 : La réciproque du th 2 est vraie aussi.
Admis.
Th 4. Si deux triangles ont un angle égale et les deux côtés adjacents proportionnels alors ils sont semblables.
Admis.
IV Exercices rédigés. ( les trois dessins seront bientôt édités)