Géométrie dans l’espace.

11 heures

I La perspective cavalière.

Par convention, on a :

• Les segments visibles en traits pleins.
• Les segments cachés en traits pointillés.
• Deux droites parallèles sont représentées par deux droites parallèles.
• Les proportions sont respéctés.
• Les angles ne sont en vrai grandeur que sur les plans de face.

Ex : Le cube et le tétraèdre.

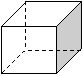
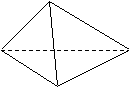
II droites et plans.

a) propriétés sur le plan :

· Trois points A , B et C non alignés définissent un unique plan noté ( ABC).

· Une droite et un point extérieur à cette droite définissent un unique plan.

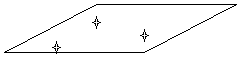
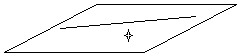
b) positions relatives d’une droite et d’un plan.

· d et P sont sécants.

L’intersection d’une droite et d’un plan est un point

· D et P sont //.

Il y a deux cas : si d est inclus dans le plan alors d // P et si d est strictement // P car d est distinct de P

Propriétés : Si une droite d est// à d1 incluse dans le plan P alors d est // P

Si une droite d est // à P alors il existe au moins une droite d1 incluse dans P qui est // à d.

Dessin :

c) Positions relatives de deux plans.

· P1 et P2 sont sécants

Proposition : L’intersection de deux plans sécants est une droite.

Dessin.

· P1 et P2 sont parallèles.

Définition : On dit que deux plans sont parallèles s’ils n’ont pas de points en commun ou s’ils sont confondus.

Rem La phrase P // Q s’il ne sont pas sécants est donc fausse.

Proposition et méthode : Si deux droites sécantes d’un plan P sont parallèles à deux droites sécantes d’un plan Q alors P et Q sont //.

Donc pour démontrer que deux plans sont // il faudra trouver deux couples de droites sécantes // deux à deux sur les plans.

Attention : Si P et Q sont // alors il est faux de dire que toute droite de P est // à toute droite de Q.

( Il suffit d’en prendre deux non coplanaire).

d) Positions relatives de deux droites.

· Elles sont coplanaires. ( Î même plan ).

Rem : On ne parle de droites sécantes ou // que si elles sont coplanaires.

Proposition : Si d et d’ sont sécantes ou parallèles alors elles sont coplanaires.

e) Non coplanaires

A savoir : Deux droites

Non coplanaires ne sont

Ni //, ni sécantes.

III Parallélisme et orthogonalité.

1. Parallélisme.

Proposition : Si deux plans sont parallèles, tout plan qui coupe l’un coupe l’autre et les droites d’intersections sont parallèles.

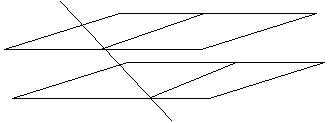
Démo : Les deux droites d et d’ sont coplanaires ( Î Q ) donc elles sont soit sécantes soit //.

Supposons qu’elles soient sécantes alors il existe un point A qui appartient en même temps aux plans P et P’ donc P et P’ sont sécants ce qui est Ø par énoncé. Donc d // d’.

( Explication du raisonnement par l’absurde).

Théorème du toit.

Si une droite d est // à deux plans sécants en d’ alors d et d’ sont //.

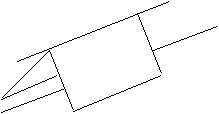
A retenir : Deux droites confondues sont dites //.

Deux droites sont // si elles sont coplanaires et sans points communs ou tous les points en communs..

2. Orthogonalité.

Proposition : Deux droites d et d’ sont orthogonales si elles sont perpendiculaires ou s’il existe d’’ // d et tel que d’’ perpendiculaire à d’.

Attention : Perpendiculaire est une notion du plan donc droites coplanaires, le symbole s’utilise toujours mais indique deux droites perpendiculaires donc coplanaires.

Proposition : Si deux droites sont orthogonales toutes // à l’une et orthogonale à l’autre.

Définition : On dit que d est perpendiculaire à P si d est orthogonale à toutes les droites du plan P.

Proposition et méthode : Pour montrer que d est perpendiculaire à P, il suffit de montrer que d est orthogonale à deux droites sécantes de P.

Rem si d et d’ sont perpendiculaire à P alors elles sont //.

IV Volumes.

Rappel des formules du prisme/ cylindre ; Pyramide/cône ; Boule.

Exercices rédigés

Comment démontrer que trois points sont alignés.

Soit P un plan et trois points A, B et C non alignés qui n’appartiennent pas à P.

(AB) coupe P en C’, (AC) coupe P en B’ et (BC) coupe P en A’.

Montrer que A’, B’ et C’ sont alignés.

Méthode : on montre qu’ils appartiennent simultanément à deux plans non confondus donc à une droite .

Comment représenter l’intersection de deux plans sécants.

Méthode : On cherche 2 ponts de cette intersections par intersection de droites .