Chap 2 représentation graphique.

Représentations graphiques Interprétation:de l'information lisible sur un graphique : valeur exacte ou approchée, influence sur l'allure de la courbe d'un changement de fenêtre graphique. Interpolation linéaire. Résolution graphique d'équations, d'inéquations et recherche d'extremum en exploitant les changements de fenêtre graphique. Lecture de courbes de niveaux et repérage d'un point par trois coordonnées.

On privilégiera les fonctions du temps. On remarquera que pour des représentations de fonctions croissantes du temps avec une graduation régulière en abscisse, on ne peut pas forcément conclure quant aux variations de [f (a+1) - f (a)]. f (a) On ne proposera aucun formalisme sur les fonctions de deux variables.

I fonctions et représentation graphiques.

.

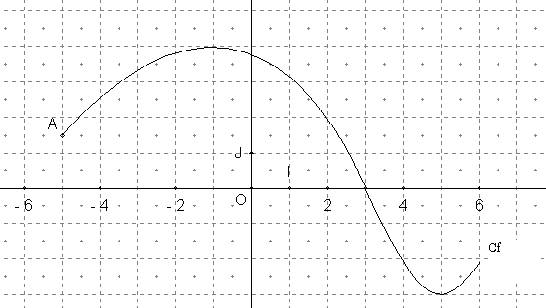
Sur le graphique, C_f est la représentation graphique d’une certaine fonction f définit sur [-5 ; 6].

(O, I, J ) permet de désigner le repère dans lequel est tracé la fonction donc on situe :

· l’origine appelée O en général,

· l’unité sur les deux axes,

L’ axe horizontal est l’axe des abscisses, noté (OI) ou encore (x’x).

L’ axe vertical est l’axe des ordonnées, noté (OJ) ou encore (y’y).

On oriente les deux axes ( flèche au bout des axes).

Ne pas oublier le titre et la légende mais aussi les échelles pour les axes.

On localise un point par une croix + et non un point, une « tache » ou encore ´, on ne trace pas les traits de construction ! Même en pointillés ! .

Sur le graphique, on peut lire que le point A a pour coordonnées ( –5 ; 1,5 ) ; on met par convention toujours l’abscisse en premier.

A est un point de la courbe tel que X_A = - 5 et Y_A = 1,5 donc on sait que f (-5 ) = 1,5.

De même D est facile à déterminer D ( 0 ; 2 ) donc on en déduit que f( 0 ) = 2.

Par contre C a pour abscisse 1 mais son ordonnée n’est pas explicitement donnée. On peut estimer qu’elle est voisine de 1,5 donc on écrira f ( 1 ) » 1,5.

Application exercice 1.

Remarque et Méthode  :

Les questions « Lire graphiquement… » et « résoudre graphiquement… » sont des énoncés analogues. La réponse se fait à partir du graphe mais il faut répondre par une phrase et laisser la preuve de la lecture sur le graphique. Pour cela, on laisse des traits en pointillés avec des flèches ( suffisamment fins pour ne pas surcharger la lecture ) qui représentent le sens de la lecture faite.

Application : Exercice 2 p 48

Vocabulaire : On dit que C_f est au dessus de Cg sur [-5 ; 6 [ si pour toute valeur de x sur [-5 ; 6[ on a f(x) ³ g(x) .

Rem : si égalité, on a des points d’intersections.

De même on dit que C_f est en dessous de Cg sur [-5 ; 6 [ si pour tout x sur [-5 ; 6 [ on a f(x) £ g(x)

Application ex 3 p48.

II sens de variation.

Sur le graphe précédent, la courbe Cf varie ( c’est à dire ‘’monte ou descend’’ ). On peut constater que sur [-5 ; -1 ] elle est croissante ( terme conventionnelle pour ‘’monte’’ ) ensuite sur [-1 ; 5] elle est décroissante (terme conventionnelle pour ‘’descend’’ ), puis sur [5 ;6] est de nouveau croissante.

Plutôt que de faire des phrases parfois longues, il est d’usage de rassembler ces informations dans un tableau dit de variation.

Valeur de x	-5 -1 5 6
Valeur de f	1,5		2

Les flèches indique le sens de variation ( croissant ou décroissant), on rajoute également les valeurs extrêmes atteintes par f : soit en –1 on a 4 et en 5 on a –3 . ce qui s’écrit plus simplement : f ( –1 ) = 4 et f( 5 ) = –3.

Rem ces deux valeurs extrémales sont dites maximales et minimales de f sur [-5 ;6].

Application : exercice 1 2^e question.

Exos 12/13/14/15 page 55.

III Lecture graphique.

Méthode 1 :

Pour résoudre graphiquement f(x) = a, il faut tracer la droite d’équation d : y = a ( en pointillé) puis lire les abscisses ( il peut y en avoir 0 ou 1 ou plusieurs ) des points d’intersections de Cf avec d. On répond à la question avec s ={ .. ; .. ; … }.

Remarque : il ne faut pas oublier les flèches de la lecture graphique.

Si a = 0 alors on recherche les points d’intersection de Cf avec l’abscisses.

Méthode 2.

Pour résoudre graphiquement f(x) < a par exemple, il faut tracer la droite d’équation d : y = a ( en pointillé) puis trouver toutes les abscisses ( il y en a une infinité en général ) des points de Cf qui sont en-dessous de d. On répond à la question avec un intervalle.

Ne pas oublier que la justification étant graphique, il doit rester une explication du travail fait sur le graphe.

IV Coordonnées en 3D.

En 2D, c’est à dire le plan, on travaille avec un repère et les coordonnées d’un point. On veut de même situé un point mais cette fois ci dans l’espace.

k

j

i

On note (O, ,, ) le repère ainsi formé.

On a l’abscisse pour i , l’ordonné pour j et la hauteur pour k.

Ex O ( 0 ;0 ;0) , I ( 1 ; 0 ; 0 ) ….