

Comment faisait-on auparavant pour calculer à la main ![]() ,
alors que de nos jours la calculatrice nous donne le résultat si facilement
?
,
alors que de nos jours la calculatrice nous donne le résultat si facilement
?
![]() On
partage le nombre dont on cherche la racine carrée en tranches de deux
chiffres à partir de la droite : 8 24 15
On
partage le nombre dont on cherche la racine carrée en tranches de deux
chiffres à partir de la droite : 8 24 15
![]() On
cherche le plus grand nombre entier dont le carré est inférieur
au nombre de la première tranche (8 ) : c'est 2 .On soustrait le carré
de ce nombre à la première tranche ( on obtient le reste partiel
)
On
cherche le plus grand nombre entier dont le carré est inférieur
au nombre de la première tranche (8 ) : c'est 2 .On soustrait le carré
de ce nombre à la première tranche ( on obtient le reste partiel
)

![]() On
abaisse le nombre correspondant à la deuxième tranche . Dans la
case de droite , on écrit le double du nombre figurant à la place
de la racine carrée.
On
abaisse le nombre correspondant à la deuxième tranche . Dans la
case de droite , on écrit le double du nombre figurant à la place
de la racine carrée.
![]() On
cherche le plus grand chiffre(?) vérifiant
On
cherche le plus grand chiffre(?) vérifiant ![]() :
c'est 8 .On écrit le 8 dans la case "racine" et on soustrait
424 - 384 = 40 ( deuxième reste partiel )
:
c'est 8 .On écrit le 8 dans la case "racine" et on soustrait
424 - 384 = 40 ( deuxième reste partiel )
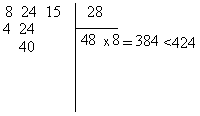
![]() On
abaisse le nombre correspondant à la troisième tranche . Dans
la case de droite , on écrit le double du nombre figurant à la
place de la racine carrée: 56
On
abaisse le nombre correspondant à la troisième tranche . Dans
la case de droite , on écrit le double du nombre figurant à la
place de la racine carrée: 56
![]() On
cherche le plus grand chiffre(?) vérifiant
On
cherche le plus grand chiffre(?) vérifiant ![]() :
c'est 7 .On écrit le 7 dans la case "racine" et on soustrait
4 015- 3 969 = 46 ( troisième reste partiel )
:
c'est 7 .On écrit le 7 dans la case "racine" et on soustrait
4 015- 3 969 = 46 ( troisième reste partiel )
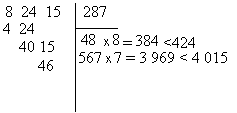
![]() On
continue ainsi de suite en ajoutant une virgule au résultat , deux zéros
pour chaque tranche ....
On
continue ainsi de suite en ajoutant une virgule au résultat , deux zéros
pour chaque tranche ....
Merci à nos calculatrices de nous donner si vite les résultats !!!!
![]() Essayons
de justifier une telle méthode ( la méthode paraissant bizarre
et compliquée , la justification peut l'être aussi ! ) :
Essayons
de justifier une telle méthode ( la méthode paraissant bizarre
et compliquée , la justification peut l'être aussi ! ) :
Supposons ( pour simplifier les choses ) que la racine carrée d'un nombre soit formée de deux chiffres "du" ( oublions ici la partie décimale ) :
Le nombre de départ est donc égal à (du)².On peut transformer (du)² de la façon suivante :
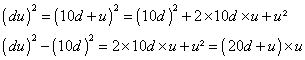
On retrouve bien la méthode effectuée ensuite à chaque
étape en étape : on cherche le nombre u tel que ![]() ,
le reste étant égal à
,
le reste étant égal à ![]() .
.